


Высшая математика – просто и доступно! 
 Вы находитесь на зеркале сайта mathprofi.ru
Вы находитесь на зеркале сайта mathprofi.ru
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Логарифмическая производная
Производные неявной, параметрической функций
Простейшие задачи
с производной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Предел функции двух переменных.
Понятие и примеры решений
Добро пожаловать на третий урок по теме ФНП, где наконец-то начали сбываться все ваши опасения =) Как многие подозревали, понятие предела распространяется и на функцию ![]() произвольного количества аргументов, в чём нам сегодня и предстоит разобраться. Однако есть оптимистичная новость. Она состоит в том, что при
произвольного количества аргументов, в чём нам сегодня и предстоит разобраться. Однако есть оптимистичная новость. Она состоит в том, что при ![]() предел в известной степени абстрактен и соответствующие задания крайне редко встречаются на практике. В этой связи наше внимание будет сосредоточено на пределах функции
предел в известной степени абстрактен и соответствующие задания крайне редко встречаются на практике. В этой связи наше внимание будет сосредоточено на пределах функции ![]() двух переменных или, как мы чаще её записываем:
двух переменных или, как мы чаще её записываем: ![]() .
.
Многие идеи, принципы и методы схожи с теорией и практикой «обычных» пределов, а значит, на данный момент вы должны уметь находить пределы и самое главное ПОНИМАТЬ, что такое предел функции одной переменной. И, коль скоро судьба привела вас на эту страничку, то, скорее всего, уже немало понимаете-умеете. А если и нет – ничего страшного, все пробелы реально заполнить в считанные часы и даже минуты.
События этого занятия разворачиваются в нашем трёхмерном мире, и поэтому будет просто огромным упущением не принять в них живое участие. Сначала соорудим хорошо известную декартову систему координат в пространстве. Давайте встанем и немного походим по комнате… …пол, по которому вы ходите – это плоскость ![]() . Поставим где-нибудь ось
. Поставим где-нибудь ось ![]() … ну, например, в любом углу, чтобы не мешалась на пути. Отлично. Теперь, пожалуйста, посмотрите вверх и представьте, что там зависло расправленное одеяло. Это поверхность, заданная функцией
… ну, например, в любом углу, чтобы не мешалась на пути. Отлично. Теперь, пожалуйста, посмотрите вверх и представьте, что там зависло расправленное одеяло. Это поверхность, заданная функцией ![]() . Наше перемещение по полу, как нетрудно понять, имитирует изменение независимых переменных
. Наше перемещение по полу, как нетрудно понять, имитирует изменение независимых переменных ![]() , и мы можем передвигаться исключительно под одеялом, т.е. в области определения функции двух переменных. Но самое интересное только начинается. Прямо над кончиком вашего носа по одеялу ползает маленький тараканчик, куда вы – туда и он. Назовём его Фредди. Его перемещение имитирует изменение соответствующих значений
, и мы можем передвигаться исключительно под одеялом, т.е. в области определения функции двух переменных. Но самое интересное только начинается. Прямо над кончиком вашего носа по одеялу ползает маленький тараканчик, куда вы – туда и он. Назовём его Фредди. Его перемещение имитирует изменение соответствующих значений ![]() функции (за исключением тех случаев, когда поверхность либо её фрагменты параллельны плоскости
функции (за исключением тех случаев, когда поверхность либо её фрагменты параллельны плоскости ![]() и высота не меняется). Уважаемый читатель с именем Фредди, не обижайся, так надо для науки.
и высота не меняется). Уважаемый читатель с именем Фредди, не обижайся, так надо для науки.
Возьмём в руки шило и проткнём одеяло в произвольной точке, высоту которой обозначим через ![]() , после чего строго под отверстием воткнём инструмент в пол – это будет точка
, после чего строго под отверстием воткнём инструмент в пол – это будет точка ![]() . Теперь начинаем бесконечно близко приближаться к данной точке
. Теперь начинаем бесконечно близко приближаться к данной точке ![]() , причём приближаться мы имеем право ПО ЛЮБОЙ траектории (каждая точка которой, разумеется, входит в область определения). Если ВО ВСЕХ случаях Фредди будет бесконечно близко подползать к проколу на высоту
, причём приближаться мы имеем право ПО ЛЮБОЙ траектории (каждая точка которой, разумеется, входит в область определения). Если ВО ВСЕХ случаях Фредди будет бесконечно близко подползать к проколу на высоту ![]() и ИМЕННО НА ЭТУ ВЫСОТУ, то функция
и ИМЕННО НА ЭТУ ВЫСОТУ, то функция ![]() имеет предел в точке
имеет предел в точке ![]() при
при ![]() :
:
![]()
Если при указанных условиях проколотая точка расположена на краю одеяла, то предел всё равно будет существовать – важно, чтобы в сколь угодно малой окрестности острия шила были хоть какие-то точки из области определения функции. Кроме того, как и в случае с пределом функции одной переменной, не имеет значения, определена ли функция ![]() в точке
в точке ![]() или нет. То есть наш прокол можно залепить жвачкой (считать, что функция двух переменных непрерывна) и это не повлияет на ситуацию – вспоминаем, что сама суть предела подразумевает бесконечно близкое приближение, а не «точный заход» в точку.
или нет. То есть наш прокол можно залепить жвачкой (считать, что функция двух переменных непрерывна) и это не повлияет на ситуацию – вспоминаем, что сама суть предела подразумевает бесконечно близкое приближение, а не «точный заход» в точку.
Однако безоблачная жизнь омрачается тем фактом, что в отличие от своего младшего брата, предел ![]() гораздо более часто не существует. Это связано с тем, что к той или иной точке на плоскости
гораздо более часто не существует. Это связано с тем, что к той или иной точке на плоскости ![]() обычно существует очень много путей, и каждый из них должен приводить Фредди строго к проколу (опционально «залепленному жвачкой») и строго на высоту
обычно существует очень много путей, и каждый из них должен приводить Фредди строго к проколу (опционально «залепленному жвачкой») и строго на высоту ![]() . А причудливых поверхностей с не менее причудливыми разрывами хоть отбавляй, что приводит к нарушению этого жёсткого условия в некоторых точках.
. А причудливых поверхностей с не менее причудливыми разрывами хоть отбавляй, что приводит к нарушению этого жёсткого условия в некоторых точках.
Организуем простейший пример – возьмём в руки нож и разрежем одеяло таким образом, чтобы проколотая точка лежала на линии разреза. Заметьте, что предел ![]() всё ещё существует, единственное, мы потеряли право ступать в точки под линией разреза, так как этот участок «выпал» из области определения функции. Теперь аккуратно приподнимем левую часть одеяла вдоль оси
всё ещё существует, единственное, мы потеряли право ступать в точки под линией разреза, так как этот участок «выпал» из области определения функции. Теперь аккуратно приподнимем левую часть одеяла вдоль оси ![]() , а правую его часть, наоборот – сдвинем вниз или даже оставим её на месте. Что изменилось? А принципиально изменилось следующее: если сейчас мы будем подходить к точке
, а правую его часть, наоборот – сдвинем вниз или даже оставим её на месте. Что изменилось? А принципиально изменилось следующее: если сейчас мы будем подходить к точке ![]() слева, то Фредди окажется на бОльшей высоте, чем, если бы мы приближались к данной точке справа. Таким образом, предела
слева, то Фредди окажется на бОльшей высоте, чем, если бы мы приближались к данной точке справа. Таким образом, предела ![]() не существует.
не существует.
Рассмотрим фрагмент плоскости ![]() :
:

Очевидно, что предел функции ![]() существует в любой конечной точке
существует в любой конечной точке ![]() плоскости
плоскости ![]() и первый практический приём решения точно такой же:
и первый практический приём решения точно такой же:
Сначала пытаемся выполнить прямую подстановку значений 
Например:
![]() и т.п.
и т.п.
Неопределённостей нет и пределы вычислены! Более того, если любую точку плоскости ![]() «выколоть шилом», то предел там всё равно будет существовать, но в подобных случаях как раз и появляется неопределённость.
«выколоть шилом», то предел там всё равно будет существовать, но в подобных случаях как раз и появляется неопределённость.
К слову, о неопределённостях. Отличительная особенность пределов функций нескольких переменных состоит в том, что ЗА КАЖУЩЕЙСЯ неопределённостью частенько скрывается несуществование предела, пожалуйста:
![]()
Что здесь? Неопределённость ![]() ? Или может быть предел равен нулю? …На самом деле данного предела не существует и тому есть очень простое геометрическое объяснение. Давайте посмотрим на два ближних к нам октанта (
? Или может быть предел равен нулю? …На самом деле данного предела не существует и тому есть очень простое геометрическое объяснение. Давайте посмотрим на два ближних к нам октанта (![]() ),в которых плоскость
),в которых плоскость ![]() пересекает координатную плоскость
пересекает координатную плоскость ![]() по прямой
по прямой ![]() и располагается как в верхнем, так и нижнем полупространстве. Таким образом, если мы будем уходить по обеим переменным на «плюс бесконечность», то Фредди может приближаться по «серой» поверхности, как к «плюс», так и к «минус бесконечности», а также ползти по прямой
и располагается как в верхнем, так и нижнем полупространстве. Таким образом, если мы будем уходить по обеим переменным на «плюс бесконечность», то Фредди может приближаться по «серой» поверхности, как к «плюс», так и к «минус бесконечности», а также ползти по прямой ![]() на нулевой высоте. Или вообще петлять туда-сюда – это зависит от нашего маршрута в плоскости
на нулевой высоте. Или вообще петлять туда-сюда – это зависит от нашего маршрута в плоскости ![]() . Следовательно, с пределом
. Следовательно, с пределом ![]() дела плохи.
дела плохи.
По той же причине, не существует и предела ![]() (два дальних от нас октанта).
(два дальних от нас октанта).
А вот с пределом ![]() всё отлично – при
всё отлично – при ![]() поверхность
поверхность ![]() расположена выше плоскости
расположена выше плоскости ![]() (левый верхний октант) и нигде не ограничена сверху, поэтому при
(левый верхний октант) и нигде не ограничена сверху, поэтому при ![]() Фредди по-любому уползёт на «плюс бесконечность». Собственно, это легко показать и аналитически:
Фредди по-любому уползёт на «плюс бесконечность». Собственно, это легко показать и аналитически:
![]()
«Зеркальный» предел ![]() проанализируйте самостоятельно.
проанализируйте самостоятельно.
…как же всё таки удобно говорить «Фредди» вместо «соответствующие значения функции» =)
Пожалуйста, «сфотографируйте» другие типовые примеры, в которых неопределённость лишь КАЖЕТСЯ, но в действительности же пределов не существует:
![]()
И на всякий случай отмечу, что перечисленные функции сами по себе не являются какими-то «прокажёнными», то есть во многих других точках с пределами полный порядок, например: ![]() и т.д.
и т.д.
Строгое определение предела функции двух переменных даётся по аналогии определения предела функции одной переменной. Подход Эдуарда Гейне заключается в рассмотрении последовательностей точек ![]() , стремящихся к
, стремящихся к ![]() , и соответствующих последовательностей значений функций
, и соответствующих последовательностей значений функций ![]() , стремящихся к
, стремящихся к ![]() . Предел по Коши определяется всё теми же окрестностями, но в пространственном случае за
. Предел по Коши определяется всё теми же окрестностями, но в пространственном случае за ![]() -окрестность обычно выбирают круг либо прямоугольник с центром в точке
-окрестность обычно выбирают круг либо прямоугольник с центром в точке ![]() , а
, а ![]() -окрестность представляет собой целый «слой», заключенный между плоскостями
-окрестность представляет собой целый «слой», заключенный между плоскостями ![]() . Точные формулировки можно найти, например, у Бохана либо Фихтенгольца, и если вы усвоили минимальные теоретические сведения о пределах, то никаких трудностей возникнуть не должно. Более обстоятельный материал есть в учебнике Ильина/Садовничего и К, где детально рассматривается в том числе и обобщенный случай предела функции в
. Точные формулировки можно найти, например, у Бохана либо Фихтенгольца, и если вы усвоили минимальные теоретические сведения о пределах, то никаких трудностей возникнуть не должно. Более обстоятельный материал есть в учебнике Ильина/Садовничего и К, где детально рассматривается в том числе и обобщенный случай предела функции в ![]() пространстве. Кстати, не надо слишком сильно смеяться над моими тараканами – во время путешествия под одеялом я рассказал вам побольше, чем типовой кирпич по математическому анализу ;-) Но всё это, конечно, было в описательном плане – исключительно для понимания. Хотя определение предела по Гейне в такой интерпретации выглядит действительно смешно =)
пространстве. Кстати, не надо слишком сильно смеяться над моими тараканами – во время путешествия под одеялом я рассказал вам побольше, чем типовой кирпич по математическому анализу ;-) Но всё это, конечно, было в описательном плане – исключительно для понимания. Хотя определение предела по Гейне в такой интерпретации выглядит действительно смешно =)
Ну а сейчас мы переходим к обширному практическому материалу, и первые примеры будут посвящены заигранным баянам, которые встречаются не только на практике, но и в учебной литературе:
Пример 1
Найти предел функции
![]()
После прямой подстановки значений ![]() в выражение под значком предела получается подлежащая ликвидации неопределённость
в выражение под значком предела получается подлежащая ликвидации неопределённость ![]() . Прежде всего, обратим внимание, что поверхность
. Прежде всего, обратим внимание, что поверхность ![]() терпит разрыв в единственной точке. И действительно, равенство
терпит разрыв в единственной точке. И действительно, равенство ![]() выполняется только в начале координат. Но существует ли там предел?
выполняется только в начале координат. Но существует ли там предел?
Проведём небольшое исследование. Сначала начнём приближаться к точке ![]() по оси абсцисс
по оси абсцисс ![]() (синяя стрелка).
(синяя стрелка).
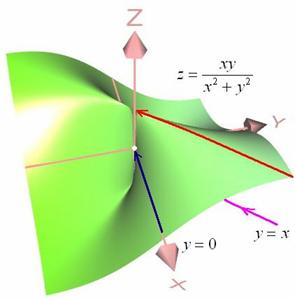
На схематическом чертеже хорошо видно, что соответствующие значения функции приближаются к нулю – ведь поверхность явно проходит через ось ![]() . Но иногда явное оказывается вовсе не явным ;-), и возникает вопрос: как в этом удостовериться аналитически? Очень просто – подставим в функцию
. Но иногда явное оказывается вовсе не явным ;-), и возникает вопрос: как в этом удостовериться аналитически? Очень просто – подставим в функцию ![]() и вычислим предел по данному пути:
и вычислим предел по данному пути:
![]() – обратите внимание, что никакой неопределённости тут нет: ноль, делённый на бесконечно малое число, равен осязаемому и железобетонному нулю.
– обратите внимание, что никакой неопределённости тут нет: ноль, делённый на бесконечно малое число, равен осязаемому и железобетонному нулю.
Теперь будем приближаться к началу координат по прямой ![]() (малиновая линия) и выясним, куда же приползёт Фредди. Судя по чертежу, куда-то выше (красная стрелка), хотя опять же не факт – вдруг там поверхность «ныряет» к нулю? Вычислим предел в предположении, что
(малиновая линия) и выясним, куда же приползёт Фредди. Судя по чертежу, куда-то выше (красная стрелка), хотя опять же не факт – вдруг там поверхность «ныряет» к нулю? Вычислим предел в предположении, что ![]() :
:

В результате получены разные числа, что противоречит определению предела, согласно которому ЛЮБОЙ допустимый маршрут к точке ![]() должен приводить Фредди к какому-то одному значению
должен приводить Фредди к какому-то одному значению ![]() . Таким образом, данного предела не существует. Вблизи точки разрыва поверхность бесконечно близко приближается («стягивается») к оси
. Таким образом, данного предела не существует. Вблизи точки разрыва поверхность бесконечно близко приближается («стягивается») к оси ![]() на различных высотах.
на различных высотах.
Но с этим примером нам повезло – совершено понятно, что в общем случае различные прямые можно перебирать до бесконечности и поэтому рациональнее проверить сразу весь «пучок» ![]() . Это множество вкупе с уравнением оси ординат
. Это множество вкупе с уравнением оси ординат ![]() учитывает все прямые пути подхода к началу координат. Оформляем решение:
учитывает все прямые пути подхода к началу координат. Оформляем решение:
![]()
Проведём замену ![]()

Результат зависит от коэффициента ![]() , следовательно, данного предела не существует.
, следовательно, данного предела не существует.
Готово!
Подставляя конкретные значения углового коэффициента, можно вычислить, на какой высоте Фредди будет приближаться к оси аппликат, если мы будем подходить к началу координат по той или иной прямой. В коварном случае потребуется дополнительно исследовать уравнение ![]() (которое не входит в семейство
(которое не входит в семейство ![]() ) но здесь до этого просто не дошло дело.
) но здесь до этого просто не дошло дело.
! Внимание! Иногда встречаются задачи, в которых требуется вычислить предел ТОЛЬКО по какой-либо линии, и, повторю очевидный факт: несмотря на отсутствие общего предела, предел по какому-либо частному направлению может себе преспокойно существовать. Например:
вычислим предел ![]() по прямой
по прямой ![]() :
:
 ;
;
теперь выясним, чему равен тот же предел, если приближаться к началу координат по параболе ![]() :
:
 и т.д.
и т.д.
Однако по многим маршрутам не существует даже и частного предела. Например, если мы приближаемся к нулю по «петляющей» траектории.
И из вышесказанного легко понять серьёзный недостаток рассмотренного метода решения: строго говоря, он пригоден лишь для обоснования НЕСУЩЕСТВОВАНИЯ предела. Ведь если мы выясним, что Фредди попадает на одну и ту же высоту ![]() по любой прямой, то этого ещё не достаточно. Согласно определению предела, нужно показать, что такой же результат получится и при ЛЮБОМ ДРУГОМ способе подхода к предельной точке. Этот вопрос решается с помощью перехода к полярным координатам.
по любой прямой, то этого ещё не достаточно. Согласно определению предела, нужно показать, что такой же результат получится и при ЛЮБОМ ДРУГОМ способе подхода к предельной точке. Этот вопрос решается с помощью перехода к полярным координатам.
Заодно вспомним метод замены в пределе:
![]()
Перейдём к полярной системе координат:
![]()
Если ![]() , то полярному радиусу ничего не остаётся, как тоже стремиться к нулю:
, то полярному радиусу ничего не остаётся, как тоже стремиться к нулю: ![]() , что совершенно естественно. Вот так вот две переменные превращаются в одну!
, что совершенно естественно. Вот так вот две переменные превращаются в одну!
![]()
Результат зависит от «угла атаки», следовательно, предела не существует.
При этом заметьте, что здесь учтены абсолютно все пути подхода к точке ![]() , поскольку полярной функцией можно задать любую прямую, кривую, ломаную, др. маршруты.
, поскольку полярной функцией можно задать любую прямую, кривую, ломаную, др. маршруты.
Но не всё в мире пределов так безрадостно:
Пример 2
Найти предел функции

Предложенная функция тоже терпит разрыв в начале координат, и предел может, как существовать, так и не существовать.
Как лучше решать подобные пределы? С моей точки зрения, выгодно придерживаться следующей тактики: сначала на черновике быстренько исследуем все прямые пути:

Проведём замену: ![]()

Предел не зависит от углового коэффициента прямой, по которой мы приближаемся к точке ![]() . Но расслабляться ещё рано! Не забываем, что в пучок прямых
. Но расслабляться ещё рано! Не забываем, что в пучок прямых ![]() не входит ось ординат! И поэтому уравнение
не входит ось ординат! И поэтому уравнение ![]() подлежит отдельному исследованию. Проще всего подставить данное значение в исходный предел:
подлежит отдельному исследованию. Проще всего подставить данное значение в исходный предел:

Если бы с помощью этого «полуметода» нам удалось установить несуществование предела (что бывает довольно часто), то получилось бы самое простое и короткое решение! Однако в данном случае проверка сработала «вхолостую», и на чистовике решение следует оформить «полноценным» способом:

Перейдём к полярным координатам: ![]()
Если ![]() , то
, то ![]()
![]()
Готово! Предел не зависит от угла ![]() , а значит и от маршрута, по которому мы приближаемся к началу координат. И особенно приятно, что полярные координаты учитывают ось ординат, с которой не пришлось возиться отдельно.
, а значит и от маршрута, по которому мы приближаемся к началу координат. И особенно приятно, что полярные координаты учитывают ось ординат, с которой не пришлось возиться отдельно.
Перед вами хорошо знакомое «проколотое одеяло»:
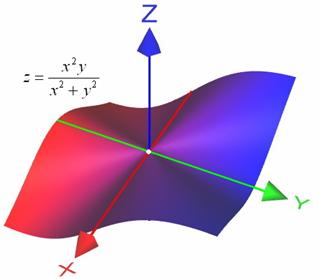
Пара пределов для самостоятельного решения:
Пример 3
Найти пределы функций
а) 
б) 
Советую не пренебрегать рассматриваемыми пределами, поскольку один, а скорее, несколько из них стопроцентно встретятся в вашей самостоятельной/контрольной работе по теме. Как вариант, «начинка» таких пределов может быть «укомплектована» множителями-константами, что принципиально не меняет результатов. Примерный образец чистового оформления в конце урока.
Рассмотрим более коварное задание:
Пример 4
Найти предел или доказать, что его не существует
![]()
Отличительная особенность предложенной функции состоит в том, что она терпит разрыв не в единичной точке, а по кубической параболе ![]() , и поэтому в данном примере возникает одна тонкость – здесь нехорошо говорить о том, что мы «приближаемся к точке
, и поэтому в данном примере возникает одна тонкость – здесь нехорошо говорить о том, что мы «приближаемся к точке ![]() по ПРЯМЫМ
по ПРЯМЫМ ![]() ». Ведь прямые этого пучка (за исключением оси абсцисс) пересекают кубическую параболу более 1-го раза и на наших путях к началу координат будут «выколотые» точки, что делает эти маршруты нелегальными.
». Ведь прямые этого пучка (за исключением оси абсцисс) пересекают кубическую параболу более 1-го раза и на наших путях к началу координат будут «выколотые» точки, что делает эти маршруты нелегальными.
Тем не менее, замена ![]() всё же возможна, но подразумевать она будет лишь участки прямых (даже очень малые), по которым мы можем беспрепятственно дойти до точки
всё же возможна, но подразумевать она будет лишь участки прямых (даже очень малые), по которым мы можем беспрепятственно дойти до точки ![]()
Все эти выкладки, конечно, не нужно «вываливать на голову» рецензента – лучше использовать обтекаемую «техническую» фразу:
Проведём замену ![]() :
:
![]()
Вроде бы тишь да гладь – предел не зависит от значения ![]() .
.
И если сейчас проявить небрежность, то он ответ будет неверным!
Не забываем, что у нас ещё не учтён путь по оси ![]() (фраза корректна!):
(фраза корректна!):
![]()
Вот тебе и раз! Как говорится, где тонко, там и рвётся.
Вывод: предела не существует
Интересно отметить, что метод перехода к полярным координатам (а его можно использовать) здесь очень опасен! После стандартной замены получается предел ![]() , который вовсе не равен тройке! При значениях угла
, который вовсе не равен тройке! При значениях угла ![]() (которые как раз и определяют ось ординат) в пределе получается ноль, и этот факт очень легко упустить из вида.
(которые как раз и определяют ось ординат) в пределе получается ноль, и этот факт очень легко упустить из вида.
Примечание: при подстановке этих значений «фи» в числителе получается ноль, а в знаменателе бесконечно малое значение, и при делении получается именно ноль – неопределённости ![]() тут нет !
тут нет !
Никогда не спешите и будьте очень внимательными!
И ещё пара важных абзацев, которые появились благодаря вам:
Поступил вопрос: а почему, в качестве пути приближения к предельной точке, мы безвариантно выбираем ![]() ? Потому что в большинстве примеров это просто удобно. Вообще, для доказательства несуществования общего предела достаточно найти ДВА произвольных маршрута, по которым получаются разные значения. Так, в разобранном примере можно было взять не весь пучок прямых, а лишь ось абсцисс + ось ординат. Кстати, это единственные «чистые» пути, и здесь как раз можно смело заявить, что мы «приближаемся к точке
? Потому что в большинстве примеров это просто удобно. Вообще, для доказательства несуществования общего предела достаточно найти ДВА произвольных маршрута, по которым получаются разные значения. Так, в разобранном примере можно было взять не весь пучок прямых, а лишь ось абсцисс + ось ординат. Кстати, это единственные «чистые» пути, и здесь как раз можно смело заявить, что мы «приближаемся к точке ![]() по прямым
по прямым ![]() ». Более того, если в пределе удобнее использовать путь, например, по параболе
». Более того, если в пределе удобнее использовать путь, например, по параболе ![]() и синусоиде
и синусоиде ![]() , то флаг вам в руки!
, то флаг вам в руки!
И важнейший момент состоит в том, что пучок ![]() годится лишь для исследования начала координат! Если переменные стремятся к другой точке, то нужно взять другой пучок, прямые которого проходят именно через эту точку.
годится лишь для исследования начала координат! Если переменные стремятся к другой точке, то нужно взять другой пучок, прямые которого проходят именно через эту точку.
Спасибо и ещё раз спасибо!
Подумайте, порешайте самостоятельно:
Пример 5
Найти предел или доказать, что его не существует

Моя версия решения в конце урока.
И как раз другие пути становятся актуальны, если аргументы (или один из них) стремятся к бесконечности:
Пример 6
Найти предел

Здесь выбор пути в плоскости ![]() влияет на порядок роста числителя и знаменателя, отчего предел может запросто не существовать. Так, если приближаться к бесконечности по прямой
влияет на порядок роста числителя и знаменателя, отчего предел может запросто не существовать. Так, если приближаться к бесконечности по прямой ![]() , то:
, то:
 (знаменатель более высокого порядка роста, чем числитель).
(знаменатель более высокого порядка роста, чем числитель).
Но если приближаться к бесконечности по параболе ![]() , то числитель и знаменатель будут одного порядка роста, а значит, предел равен ненулевому значению:
, то числитель и знаменатель будут одного порядка роста, а значит, предел равен ненулевому значению:

Вывод: общего предела  не существует.
не существует.
И в случае несущестования предела лучше использовать именно этот способ! Засада в том, что переход к полярным координатам тут совсем плохо отображает ситуацию, и во многих случаях замена приведёт к ошибочному выводу. Но есть и исключения, например, многострадальная функция ![]() , где после перехода получится результат, зависящий только от «фи».
, где после перехода получится результат, зависящий только от «фи».
Контрпример 6+
![]()
Анализируя «начинку» предела, появляются веские основания полагать, что какой бы маршрут мы ни выбрали – порядок роста числителя всегда будет меньше порядка роста знаменателя, следовательно, предел равен нулю.
И вот здесь перейдем к полярной системе координат:
![]()
Если ![]() то
то ![]() , к слову, знак при «эр» можно и опустить.
, к слову, знак при «эр» можно и опустить.
Следует заметить, что если один или оба аргумента стремятся к «минус бесконечности», то полярный радиус всё равно будет стремиться к «плюс бесконечности» (проанализируйте, почему). Таким образом, замена пригодна для «бесконечностей» с любыми знаками, однако знаки «бесконечностей» сохраняют существенное значение, и очень скоро я вернусь к этому вопросу:
![]()
Геометрически это означает, что если мы уходим на бесконечность по направлениям ![]() , то поверхность будет бесконечно близко приближаться к плоскости
, то поверхность будет бесконечно близко приближаться к плоскости ![]() , т.е. к координатной плоскости
, т.е. к координатной плоскости ![]() . Причём, приближаться сверху: так как все дела происходят в первой координатной четверти, то
. Причём, приближаться сверху: так как все дела происходят в первой координатной четверти, то ![]() , и строго говоря, предел равен
, и строго говоря, предел равен ![]() (запись «плюс ноль» здесь символизирует приближение сверху).
(запись «плюс ноль» здесь символизирует приближение сверху).
Заметьте, что при ![]() косинус становится отрицательным, а значит, поверхность приближается к плоскости
косинус становится отрицательным, а значит, поверхность приближается к плоскости ![]() уже со стороны нижнего полупространства:
уже со стороны нижнего полупространства: ![]() (запись «минус ноль» символизирует приближение снизу).
(запись «минус ноль» символизирует приближение снизу).
В данном примере это, конечно, не имеет особого значения, поскольку предел равен нулю вообще по любым бесконечным направлениям, но в общем случае разница критична. Условный пример:
![]() , если
, если ![]() либо
либо ![]() (1-я и 2-я координатные четверти, где синус положителен);
(1-я и 2-я координатные четверти, где синус положителен);
![]() , если
, если ![]() либо
либо ![]() (3-я и 4-я координатные четверти, где синус отрицателен).
(3-я и 4-я координатные четверти, где синус отрицателен).
Таким образом, после перехода к полярным координатам нужно держать на заметке, к каким именно «бесконечностям» стремятся аргументы функции!
Для самостоятельного решения:
Пример 7
Вычислить предел

Приятный случай, когда знаки бесконечностей не важны – этот вывод следует из того, что все переменные входят в функцию в чётных степенях и, кроме того, каждое подкоренное выражение заведомо неотрицательно. Здесь можно смело переходить к полярным координатам или вообще заменить сумму квадратов одной буквой, как я и сделал в образце решения.
Помимо специфических приёмов, в ходе вычисления пределов функций двух переменных используется широкий арсенал уже известных вам методов:
Пример 8

В результате прямой подстановки ![]() сталкиваемся с неопределённостью
сталкиваемся с неопределённостью ![]() , для устранения которой перспективным выглядит разложение числителя и знаменателя на множители. В числителе используем формулу разности квадратов, а в знаменателе проводим вынесение множителей за скобки (у 1-3-го и 2-4-го слагаемых):
, для устранения которой перспективным выглядит разложение числителя и знаменателя на множители. В числителе используем формулу разности квадратов, а в знаменателе проводим вынесение множителей за скобки (у 1-3-го и 2-4-го слагаемых):

Сокращение «виновника» ![]() означает, что функция
означает, что функция ![]() терпит разрыв по типу «разрезанное одеяло» во всех точках прямой
терпит разрыв по типу «разрезанное одеяло» во всех точках прямой ![]() за исключением точки
за исключением точки ![]() . Впрочем, оставим этот материал до урока Непрерывность функции двух переменных и вернёмся к нашим баранам:
. Впрочем, оставим этот материал до урока Непрерывность функции двух переменных и вернёмся к нашим баранам:
Пример 9

Умножим числитель и знаменатель на сопряжённое выражение:

Получено нечто знакомое, и концовка решения, думаю, не нуждается в комментариях.
Перейдём к полярным координатам: ![]()
Если ![]() , то
, то ![]()
![]()
Теперь ваша парочка:
Пример 10
Найти пределы
а) 
б) ![]()
Решения занимают буквально 2-3 строчки. Если возникли затруднения с пунктом «бэ», пожалуйста, посмотрите Пример 5 статьи Сложные пределы.
И, конечно же, замечательные пределы, куда без них. Рассмотрим поучительный во всех смыслах пример:
Пример 11

Используем до боли знакомую тригонометрическую формулу ![]() , где
, где ![]() и стандартным искусственным приёмом организуем первые замечательные пределы
и стандартным искусственным приёмом организуем первые замечательные пределы ![]() :
:

Перейдём к полярным координатам: ![]()
Если ![]() , то
, то ![]()
Казалось бы, решение идёт к закономерной развязке и ничто не предвещает неприятностей, однако в самом конце существует большой риск допустить серьёзный недочёт, о характере которого я уже чуть-чуть намекнул в Примере 3 и подробно расписал после Примера 6. Сначала концовка, затем комментарий:
![]()
Давайте разберёмся, почему будет плохо записать просто «бесконечность» или «плюс бесконечность». Посмотрим на знаменатель: так как ![]() , то полярный радиус стремится к бесконечно малому положительному значению:
, то полярный радиус стремится к бесконечно малому положительному значению: ![]() . Кроме того,
. Кроме того, ![]() . Таким образом, знак знаменателя и всего предела зависит только от косинуса:
. Таким образом, знак знаменателя и всего предела зависит только от косинуса:
![]() , если полярный угол
, если полярный угол ![]() (2-я и 3-я координатные четверти:
(2-я и 3-я координатные четверти: ![]() );
);
![]() , если полярный угол
, если полярный угол ![]() (1-я и 4-я координатные четверти:
(1-я и 4-я координатные четверти: ![]() ).
).
Геометрически это означает, что если приближаться к началу координат слева, то поверхность, заданная функцией ![]() , простирается до бесконечности вниз:
, простирается до бесконечности вниз:

и если справа – то вверх:

А между погружением на дно океана и полётом за облака, мягко говоря, есть разница.
Задание для самостоятельного решения:
Пример 12

Краткое решение и ответ в концу урока. Как видите, с технической точки зрения ничего особенно нового-то, и нет.
Вместо замечательных пределов можно использовать и замечательные эквивалентности:
Пример 13

Решим это предел устно: при ![]() справедлива эквивалентность
справедлива эквивалентность ![]() . В данном случае
. В данном случае ![]() и после эквивалентной замены получаем предел
и после эквивалентной замены получаем предел  . Почему это корректно? В достаточно малой окрестности точки
. Почему это корректно? В достаточно малой окрестности точки ![]() поверхность,
поверхность, ![]() практически совпадает с поверхностью
практически совпадает с поверхностью ![]() , и поэтому одну функцию можно безболезненно заменить другой.
, и поэтому одну функцию можно безболезненно заменить другой.
На втором шаге переходим к полярным координатам, после чего ![]() превращается в
превращается в ![]() , а примелькавшаяся сумма
, а примелькавшаяся сумма ![]() – в
– в ![]() . По итогу:
. По итогу:
![]()
Желающие могут прорешать Примеры 11, 12 вторым способом, что, кстати, проще
Проверьте, насколько хорошо вы усвоили урок о бесконечно малых функциях:
Пример 14
Найти предел функции двух переменных
![]()
Решение совсем близко.
И заключительные примеры статьи посвящены второму замечательному пределу:
Пример 15

Приём решения такой же: делаем дробь трёхэтажной и искусственным возведением в степень организуем второй замечательный предел ![]() :
:

В силу непрерывности экспоненциальной функции, значок предела можно перенести в показатель: 
Чтобы не возиться с мелкими символами, предел показателя удобно вычислить отдельно:
![]()
Тут лучше использовать метод «опровержения», рассмотрев 2 пути, однако это как раз то исключение, о котором я рассказал после Примера 6. Перейдём к полярным координатам: ![]()
Если ![]() , то
, то ![]()
![]()
Результат зависит от полярного угла, поэтому предела ![]() , а значит, и предела
, а значит, и предела ![]() не существует.
не существует.
Готово!
Геометрически это означает, что в процессе приближения к бесконечности по различным направлениям угла ![]() , поверхность
, поверхность  будет бесконечно близко приближаться к различным значениям высоты
будет бесконечно близко приближаться к различным значениям высоты ![]() . Так, например, если уходить на бесконечность по прямой
. Так, например, если уходить на бесконечность по прямой ![]() , то для соответствующего угла 45 градусов:
, то для соответствующего угла 45 градусов:

И, как я уже отмечал в самом начале, на практике вам вполне могут предложить вычислить не общий предел, а предел по какому-либо частному пути, да тот же самый: «Вычислить предел  по направлению прямой
по направлению прямой ![]() ». Проблем вообще никаких:
». Проблем вообще никаких:

Существует и частный предел по «школьной» параболе ![]() , в этом случае «угол атаки»
, в этом случае «угол атаки» ![]() , и задача легко решается через полярные координаты:
, и задача легко решается через полярные координаты:

И тут следует напомнить, что предела по многим путям вовсе не существует. Например, если мы уходим на бесконечность по синусоидальному или спиралевидному маршруту. Проще всего это обосновать в полярной системе координат: угол «фи» постоянно меняется, а посему и предела нет.
На посошок:
Пример 16
Вычислить предел функции двух переменных или доказать, что его не существует:

Всё очень просто!
Материалов данного урока должно хватить для решения большинства практических примеров по теме, но, тем не менее, на следующих занятиях (Повторные пределы и Непрерывность функции двух переменных), мы продолжим работать с пределами функций двух переменных, и, более того, я расскажу вам ещё об одном эффективном методе их решения.
Спасибо за активное участие и до скорых встреч!
Решения и ответы:
Пример 3: Решение:
а) 
Функция терпит разрыв в начале координат.
Перейдём к полярным координатам: ![]()
Если ![]() , то
, то ![]()
![]()
Примечание: поскольку ![]() , то в знаменателе именно
, то в знаменателе именно ![]()
б) 
Проведём замену ![]()

Результат зависит от коэффициента ![]() , значит, данного предела не существует
, значит, данного предела не существует
Пример 5: Решение: вычислим предел по оси абсцисс:

Вычислим предел по оси ординат:

Вывод: общего предела не существует
Пример 7: Решение:

Проведём замену переменной: ![]()
Если ![]() , то
, то ![]()
![]()
Разделим числитель и знаменатель на ![]()

Пример 10: Решение:
а) 
Умножим числитель и знаменатель на сопряжённое выражение

б) ![]()
Умножим числитель и знаменатель на сопряжённое выражение

Пример 12: Решение:

Используем формулу ![]() и первый замечательный предел.
и первый замечательный предел.

Пример 14: Решение:
![]()
Поскольку ![]() и
и ![]() , то
, то ![]() ;
;
поскольку ![]() , то
, то ![]()
![]()
Проведём замену: ![]()
![]()
Результат зависит от ![]() , поэтому предела не существует.
, поэтому предела не существует.
Пример 16: Решение:

Используем 2-й замечательный предел в виде ![]()

Примечание: предел  найден в Примере 9
найден в Примере 9
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright