


Высшая математика – просто и доступно! 
 Вы находитесь на зеркале сайта mathprofi.ru
Вы находитесь на зеркале сайта mathprofi.ru
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Логарифмическая производная
Производные неявной, параметрической функций
Простейшие задачи
с производной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Геометрическое определение вероятности. Задачи с решениями
За окном ранние осенние деньки, и жёлтая листва на деревьях навевает лирическое и немного грустное настроение…. Но впереди ещё целый учебный год и в такие моменты нужно обязательно настроиться на плодотворную работу! Спешу обрадовать всех хандрящих читателей своим фирменным рецептом, позволяющим быстро повысить тонус своего организма. Для этого достаточно немножко вспомнить геометрию… …нет, я согласен, что иногда она усыпляет, но в небольших дозах – исключительно бодрит! И, главное, очень действенно – как только начинаешь принимать живительные порции знаний, так сразу никакой сезонной депрессии!
Ещё на первом уроке по теме мы познакомились с классическим определением вероятности появления некоторого события ![]() в испытании и простейшей формулой
в испытании и простейшей формулой ![]() , где
, где ![]() – общее число всех возможных равновозможных, элементарных исходов данного испытания, а
– общее число всех возможных равновозможных, элементарных исходов данного испытания, а ![]() – кол-во элементарных исходов, благоприятствующих событию
– кол-во элементарных исходов, благоприятствующих событию ![]() .
.
Возникли затруднения с терминологией и/или пониманием? Пожалуйста, начните с основ теории вероятностей.
Едем дальше: классическое определение вероятности оказывается эффективным для решения целого спектра задач, но с другой стороны, обладает и рядом недостатков. Даже правильнее сказать, не недостатков, а ограничений. Одним из таких ограничений является тот факт, что оно неприменимо к испытаниям с бесконечным количеством исходов. Простейший пример:
На отрезок ![]() наудачу бросается
наудачу бросается голодная точка. Какова вероятность того, что она попадёт в промежуток ![]() ?
?

Поскольку на отрезке бесконечно много точек, то здесь нельзя применить формулу ![]() (ввиду бесконечно большого значения «эн») и поэтому на помощь приходит другой подход, называемый геометрическим определением вероятности.
(ввиду бесконечно большого значения «эн») и поэтому на помощь приходит другой подход, называемый геометрическим определением вероятности.
Всё очень похоже: вероятность наступления некоторого события ![]() в испытании равна отношению
в испытании равна отношению ![]() , где
, где ![]() – геометрическая мера, выражающая общее число всех возможных и равновозможных исходов данного испытания, а
– геометрическая мера, выражающая общее число всех возможных и равновозможных исходов данного испытания, а ![]() – мера, выражающая количество благоприятствующих событию
– мера, выражающая количество благоприятствующих событию ![]() исходов. На практике в качестве такой геометрической меры чаще всего выступает длина или площадь, реже – объём.
исходов. На практике в качестве такой геометрической меры чаще всего выступает длина или площадь, реже – объём.
Рассмотрим событие: ![]() – брошенная на отрезок
– брошенная на отрезок ![]() точка, попала в промежуток
точка, попала в промежуток ![]() . Очевидно, что общее число исходов выражается длиной бОльшего отрезка:
. Очевидно, что общее число исходов выражается длиной бОльшего отрезка: ![]() , а благоприятствующие событию
, а благоприятствующие событию ![]() исходы – длиной вложенного отрезка:
исходы – длиной вложенного отрезка: ![]() По геометрическому определению вероятности:
По геометрическому определению вероятности:
![]()
Слишком просто? Как и в случае с классическим определением, это обманчивое впечатление. Обстоятельно и добросовестно разбираемся в практических примерах:
Задача 1
Метровую ленту случайным образом разрезают ножницами. Найти вероятность того, что длина обрезка составит не менее 80 см.
Решение: «чего тут сложного? Вероятность равна 1/5-й». Это автоматическая ошибка, которую допускают по небрежности. Да, совершенно верно – длина обрезка составит не менее 80 см, если от ленты отрезать не более 20 сантиметров. Но здесь часто забывают, что искомый разрез можно сделать как с одного конца ленты, так и с другого:
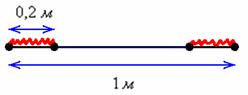
Рассмотрим событие: ![]() – длина обрезка составит не менее 0,8 м.
– длина обрезка составит не менее 0,8 м.
Поскольку ленту можно разрезать где угодно, то общему числу исходов соответствует её длина: ![]() Благоприятствующие событию
Благоприятствующие событию ![]() участки разреза отмечены на рисунке красным цветом и их суммарная длина равна:
участки разреза отмечены на рисунке красным цветом и их суммарная длина равна: ![]() По геометрическому определению:
По геометрическому определению: ![]()
Ответ: 0,4
Какой можно сделать вывод? Даже если задача кажется вам очень простой, НЕ СПЕШИТЕ. Импульсивность вообще штука скверная – это ошибки, ненужные покупки, испорченные кожные покровы отношения и т.д.… но не будем о грустном!
При оформлении задач следует обязательно указывать размерность (единицы, метры, квадратные единицы, квадратные метры и т.д.). Кстати, обратите внимание, что на финальном этапе вычислений геометрическая мера сокращается. Так в рассмотренном примере, сократились метры: ![]() , в результате чего получилась привычная безразмерная вероятность.
, в результате чего получилась привычная безразмерная вероятность.
Разминочная задача из сборника Рябушко:
Задача 2
После бури на участке между 40-м и 70-м километрами телефонной линии произошёл обрыв провода. Какова вероятность того, что он произошёл между 50-м и 55-м километрами линии?
Краткое и решение и ответ в конце урока.
Значительно чаще встречаются примеры, в которых фигурируют площади:
Задача 3
В треугольник со сторонами ![]() вписан круг. Точка
вписан круг. Точка ![]() произвольно ставится в треугольник. Найти вероятность того, что точка попадёт в круг.
произвольно ставится в треугольник. Найти вероятность того, что точка попадёт в круг.
Напоминаю, что вписанный круг лежит внутри треугольника и касается его сторон в 3 точках
Решение: поскольку точка ставится в треугольник, а круг лежит внутри, то общему числу исходов соответствует площадь треугольника, а множеству благоприятствующих исходов – площадь вписанного круга. Что тут сказать? Ищем площади:
Если даны длины сторон треугольника, то его площадь удобно найти по формуле Герона:
![]() , где
, где ![]() – длины сторон треугольника, а
– длины сторон треугольника, а ![]() – полупериметр.
– полупериметр.
Сначала вычислим полупериметр треугольника: ![]() , а затем его площадь:
, а затем его площадь: ![]()
Методику вынесения множителей из-под корня я освещал ещё в древние-древние времена на вводном уроке по аналитической геометрии.
Площадь вписанного круга найдём по формуле ![]() , где
, где ![]() – его радиус.
– его радиус.
Откуда брать геометрические формулы? Нужные формулы можно найти в школьном учебнике или другом источнике информации. При этом нет никакой необходимости специально их разучивать, лично я вспомнил только ![]() , а всё остальное в считанные минуты нашёл в Википедии. И через считанные минуты всё это благополучно забуду =)
, а всё остальное в считанные минуты нашёл в Википедии. И через считанные минуты всё это благополучно забуду =)
Итак, площадь вписанного круга: 
По геометрическому определению:
 – вероятность того, что точка
– вероятность того, что точка ![]() попадёт во вписанный круг.
попадёт во вписанный круг.
Ответ: ![]()
Более простой пример для самостоятельного решения:
Задача 4
В круге радиуса 10 см находится прямоугольный треугольник с катетами 12 и 7 см. В круг наудачу ставится точка. Найти вероятность того, что она не попадёт в данный треугольник.
Следует отметить, что в этой задаче треугольник вовсе не обязан как-то касаться окружности, он просто расположен внутри круга и всё. Будьте внимательны!
А теперь рассмотрим широко известную задачу о встрече:
Задача 5
Две грузовые машины могут подойти на погрузку в промежуток времени от 19.00 до 20.30. Погрузка первой машины длится 10 минут, второй – 15 минут. Какова вероятность того, что одной машине придется ждать окончания погрузки другой?
Давайте немного осмыслим условие. Во-первых, автомобили могут подойти на погрузку в любом порядке, а во-вторых – в любые моменты времени в течение полутора часов. По первой оглядке решение представляется довольно трудным. И для неподготовленного человека оно действительно окажется «не по зубам». Подробный анализ метода решения этой задачи можно найти, например, в учебном пособии Гмурмана, я же ограничусь в известной степени формальным алгоритмом:
Решение: сначала выясняем длительность временнОго промежутка, на котором может состояться встреча. В данном случае, как уже отмечено выше, это полтора часа или 90 минут. При этом здесь не имеют особого значения фактические временнЫе рамки – погрузка автомобилей, может состояться, например, утром с 8.30 до 10.00, и решение будет точно таким же.
Вычисления допустимо проводить как в долях часа, так и в минутах. На мой взгляд, в большинстве случаев удобнее работать с минутами – меньше путаницы.
На первом шаге изобразим прямоугольную систему координат, где в подходящем масштабе построим квадрат размером 90 на 90 единиц; при этом одна из вершин квадрата совпадает с началом координат, а его смежные стороны лежат на координатных осях.
Общему множеству исходов будет соответствовать площадь данного квадрата: ![]() Размерность лучше указать в квадратных единицах, поскольку квадратные минуты смотрятся как-то неудачно.
Размерность лучше указать в квадратных единицах, поскольку квадратные минуты смотрятся как-то неудачно.
Далее по оси ![]() от начала координат откладываем время погрузки одного автомобиля (зелёная линия), а по оси
от начала координат откладываем время погрузки одного автомобиля (зелёная линия), а по оси ![]() – время погрузки другого автомобиля (красная линия) (можно наоборот, это не повлияет на решение):
– время погрузки другого автомобиля (красная линия) (можно наоборот, это не повлияет на решение):

Теперь из правого конца зелёного отрезка и из верхнего конца красного отрезка под углом 45 градусов проводим две линии внутри квадрата (малиновые отрезки).
Множеству благоприятствующих исходов (когда автомобили «пересекутся» во времени) соответствует площадь ![]() заштрихованной фигуры. В принципе, её можно вычислить «на пальцах», но технически проще найти площади двух прямоугольных треугольников с помощью формулы
заштрихованной фигуры. В принципе, её можно вычислить «на пальцах», но технически проще найти площади двух прямоугольных треугольников с помощью формулы ![]() , где
, где ![]() – длины катетов. Обратите внимание, что в общем случае эти треугольники не равны. У нас: верхний треугольник имеет катеты длиной по 80 единиц, нижний треугольник – по 75 единиц. Таким образом, суммарная площадь треугольников составляет:
– длины катетов. Обратите внимание, что в общем случае эти треугольники не равны. У нас: верхний треугольник имеет катеты длиной по 80 единиц, нижний треугольник – по 75 единиц. Таким образом, суммарная площадь треугольников составляет:
![]()
И бесхитростный заключительный манёвр: из площади квадрата вычитаем площади треугольников, получая тем самым благоприятствующую площадь:
![]()
По геометрическому определению:
![]() – вероятность того, что одной машине придется ждать окончания погрузки другой.
– вероятность того, что одной машине придется ждать окончания погрузки другой.
Ответ: ![]()
Если в разобранной задаче встреча была явно нежелательна, то в следующей – скорее, наоборот =) Романтичный эпизод для самостоятельного изучения:
Задача 6
Студенты случайным образом приходят в столовую с 14.00 до 15.00, при этом обед каждого из них занимает примерно 20 минут. Найти вероятность того, что: а) Коля встретится с Олей во время обеда, б) данная встреча не состоится.
Не нужно печалиться по поводу пункта «бэ» – любовь приходит и уходит, а кушать хочется всегда! …прошу прощения за тонкий юмор =) Решение, чертёж и ответ в конце урока.
Оставшиеся примеры статьи посвящены не менее распространённой задаче на геометрическое определение вероятности. Для начала заманивающий пример:
Задача 7
В квадрат с вершинами ![]() наудачу брошена точка
наудачу брошена точка ![]() . Найдите вероятность того, что координаты этой точки удовлетворяют неравенству
. Найдите вероятность того, что координаты этой точки удовлетворяют неравенству![]() .
.
Решение: изобразим на чертеже искомый квадрат и прямую ![]() :
:
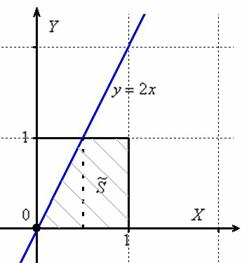
Общему множеству исходов соответствует площадь квадрата ![]()
Прямая ![]() делит квадрат на треугольник и трапецию. Как определить фигуру, которая удовлетворяет условию
делит квадрат на треугольник и трапецию. Как определить фигуру, которая удовлетворяет условию ![]() ? Вспоминаем линейные неравенства: нужно взять любую точку, не принадлежащую прямой
? Вспоминаем линейные неравенства: нужно взять любую точку, не принадлежащую прямой ![]() , например, точку
, например, точку ![]() и подставить её координаты в неравенство:
и подставить её координаты в неравенство:
![]()
Получено верное неравенство, значит, множеству благоприятствующих исходов соответствует площадь ![]() трапеции. Рассчитаем данную площадь как сумму площадей прямоугольного треугольника и прямоугольника:
трапеции. Рассчитаем данную площадь как сумму площадей прямоугольного треугольника и прямоугольника:
![]()
По геометрическому определению:
 – вероятность того, что координаты брошенной в данный квадрат точки удовлетворяют неравенству
– вероятность того, что координаты брошенной в данный квадрат точки удовлетворяют неравенству![]() .
.
Ответ: ![]()
…я так и знал, что вы соскучились по неравенствам =) А они бывают не только линейными:
Задача 8
Загадываются два числа ![]() и
и ![]() в промежутке от 0 до 5. Какова вероятность, что
в промежутке от 0 до 5. Какова вероятность, что ![]() ?
?
Схема решения уже знакома: коль скоро загадываются 2 произвольных числа от нуля до пяти (они могут быть и иррациональными), то общему количеству исходов соответствует площадь квадрата ![]()
Изобразим ветвь гиперболы ![]() , которая делит квадрат на две части:
, которая делит квадрат на две части:
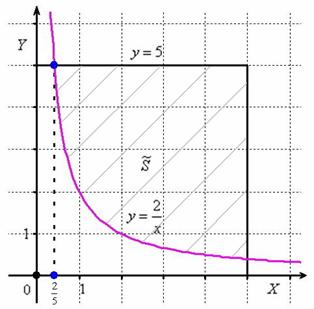
Теперь выясним, какой из этих двух «кусков» удовлетворяет неравенству ![]() . Для этого выберем любую точку, не принадлежащую гиперболе, проще всего взять
. Для этого выберем любую точку, не принадлежащую гиперболе, проще всего взять ![]() , и подставим её координаты в наше неравенство:
, и подставим её координаты в наше неравенство:
![]()
Получено неверное неравенство, а значит, условию ![]() соответствует «верхний кусок», площадь
соответствует «верхний кусок», площадь ![]() которого вычислим с помощью определённого интеграла.
которого вычислим с помощью определённого интеграла.
Уточним нижний предел интегрирования аналитически (найдём точку пересечения гиперболы ![]() и прямой
и прямой ![]() ):
):
![]()
На отрезке ![]() прямая
прямая ![]() расположена не ниже гиперболы
расположена не ниже гиперболы ![]() ,
,
по соответствующей формуле:

По геометрическому определению:
 – вероятность того, что произведение двух загаданных в промежутке от 0 до 5 чисел окажется больше двух.
– вероятность того, что произведение двух загаданных в промежутке от 0 до 5 чисел окажется больше двух.
Ответ: ![]()
Аналогичный пример для самостоятельного решения:
Задача 9
Загадываются два числа ![]() и
и ![]() в промежутке от 0 до 10. Какова вероятность, что
в промежутке от 0 до 10. Какова вероятность, что ![]() ?
?
Данная задача (как, собственно, и предыдущая) допускает несколько способов расчёта площади, подумайте, какой путь более рационален. Моя версия решения совсем близко.
В заключение следует отметить, что геометрическое определение вероятности тоже обладает своими недостатками. Один из них заключается в своеобразном парадоксе, давайте вспомним демонстрационный пример с отрезком ![]() , на который случайным образом падает точка. Возможно ли, что точка попадёт, например, на самый край отрезка? Да, такое событие возможно, но по геометрическому определению, его вероятность равна нулю! И то же самое можно сказать о любой точке отрезка! Дело в том, что с позиций геометрии размеры отдельно взятой точки равны нулю, и поэтому геометрическое определение вероятности здесь не срабатывает.
, на который случайным образом падает точка. Возможно ли, что точка попадёт, например, на самый край отрезка? Да, такое событие возможно, но по геометрическому определению, его вероятность равна нулю! И то же самое можно сказать о любой точке отрезка! Дело в том, что с позиций геометрии размеры отдельно взятой точки равны нулю, и поэтому геометрическое определение вероятности здесь не срабатывает.
Надеюсь, ваше настроение значительно улучшилось и теперь вы обязательно справитесь со всеми учебными и внеучебными трудностями. …Не улучшилось?! Дополнительные задачи по теме можно найти в архиве готовых решений по сборнику Чудесенко =) =)
Везения в главном!
Решения и ответы:
Задача 2: Решение: используем геометрическое определение вероятности. Общему числу исходов соответствует участок длиной ![]() , благоприятствующему количеству исходов – участок длиной
, благоприятствующему количеству исходов – участок длиной ![]() . Таким образом:
. Таким образом:
![]() – вероятность того, что обрыв провода произошёл между 50-м и 55-м километрами линии.
– вероятность того, что обрыв провода произошёл между 50-м и 55-м километрами линии.
Ответ: ![]()
Задача 4: Решение: общему количеству исходов соответствует площадь круга:
![]()
Площадь прямоугольного треугольника равна полупроизведению его катетов:
![]()
По условию поставленная в круг точка не должна попасть в треугольник, поэтому благоприятствующее число исходов выражается разностью ![]()
По геометрическому определению:
![]() – вероятность того, что поставленная в круг точка не попадёт в треугольник.
– вероятность того, что поставленная в круг точка не попадёт в треугольник.
Ответ: ![]()
Задача 6: Решение: Оля и Коля могут встретиться в течение 60 минут. Выполним чертёж:
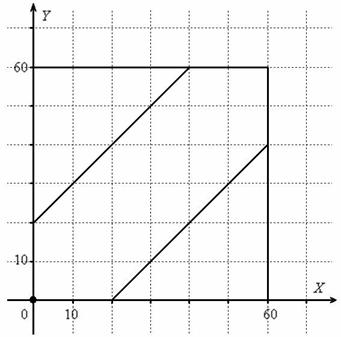
Площадь квадрата ![]() соответствует общему числу исходов.
соответствует общему числу исходов.
Рассмотрим противоположные события:
![]() – Оля и Коля встретятся во время обеда;
– Оля и Коля встретятся во время обеда;
![]() – данной встречи не состоится.
– данной встречи не состоится.
Вычислим суммарную площадь двух треугольников:
![]() – данное значение благоприятствует событию
– данное значение благоприятствует событию ![]() .
.
По геометрическому определению вероятности:
![]()
Противоположные события образуют полную группу, поэтому:
![]()
Ответ: ![]()
Задача 9: Решение: выполним чертёж:
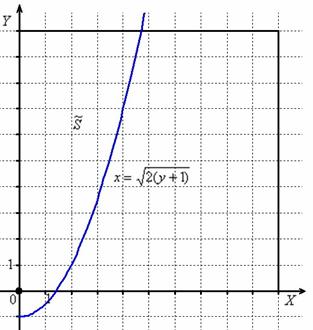
Общее число исходов выражается площадью квадрата ![]() . Неравенству
. Неравенству ![]() соответствует площадь
соответствует площадь ![]() , которую вычислим с помощью определённого интеграла, интегрируя по «игрек» (данный метод рассмотрен в статье Объем тела вращения).
, которую вычислим с помощью определённого интеграла, интегрируя по «игрек» (данный метод рассмотрен в статье Объем тела вращения).
Выразим обратную функцию: ![]() .
.
На отрезке ![]() , поэтому:
, поэтому:

По геометрическому определению:
 – вероятность того, что два загаданных от нуля до 10 числа будут удовлетворять неравенству
– вероятность того, что два загаданных от нуля до 10 числа будут удовлетворять неравенству ![]()
Ответ: 
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright