


Высшая математика – просто и доступно! 
 Вы находитесь на зеркале сайта mathprofi.ru
Вы находитесь на зеркале сайта mathprofi.ru
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Логарифмическая производная
Производные неявной, параметрической функций
Простейшие задачи
с производной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Как вычислить двойной интеграл
в полярной системе координат?
Закончим бой с двойным интегралом нокаутом в третьем раунде. Что нужно знать и уметь для полной победы? Ещё раз взглянем на заголовок статьи… очевидно, вы должны знать, что такое полярные координаты… и уметь решать двойные интегралы =) Стоп-стоп, не закрываем в панике страницу – первое осваивается в считанные минуты, ну а второе, конечно, несколько дольше. Итак, чайникам – двойные интегралы для чайников, остальных же читателей приглашаю ознакомиться с третьим уроком темы. Новизны будет совсем немного и если вы мало-мальски набили руку на вычислении двойных интегралов, то особых трудностей возникнуть не должно.
Типовое задание формулируется примерно так: «Вычислить двойной интеграл, используя полярную систему координат». После чего для решения предлагается … обычный двойной интеграл ![]() в декартовых координатах по области
в декартовых координатах по области ![]() . Сначала рассмотрим более простой и распространённый случай, когда подынтегральная функция двух переменных
. Сначала рассмотрим более простой и распространённый случай, когда подынтегральная функция двух переменных ![]() и двойной интеграл
и двойной интеграл ![]() численно равен площади области интегрирования. Разберём алгоритм решения на бесхитростной демо-задаче:
численно равен площади области интегрирования. Разберём алгоритм решения на бесхитростной демо-задаче:
Пример 1
Вычислить площадь плоской фигуры, ограниченную линиями ![]() , с помощью двойного интеграла, используя полярную систему координат
, с помощью двойного интеграла, используя полярную систему координат
Решение: На первом этапе ничего нового. Выполняем чертёж области ![]() в прямоугольной системе координат. Линейное неравенство
в прямоугольной системе координат. Линейное неравенство ![]() определяет правую полуплоскость, включая ось
определяет правую полуплоскость, включая ось ![]() , а уравнение
, а уравнение ![]() , очевидно, задаёт какую-то линию 2-го порядка. Чтобы выяснить, какую именно – выделим полный квадрат:
, очевидно, задаёт какую-то линию 2-го порядка. Чтобы выяснить, какую именно – выделим полный квадрат:

![]() – окружность единичного радиуса с центром в точке
– окружность единичного радиуса с центром в точке ![]() .
.
Таким образом, требуется вычислить площадь половинки круга:
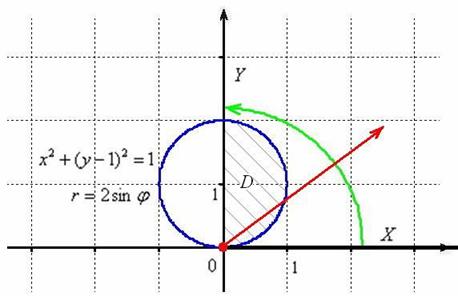
Не упустим возможность сразу узнать ответ. По школьной формуле у нас должно получиться: ![]()
Площадь фигуры стандартно рассчитывается по формуле ![]() , однако по условию нужно воспользоваться полярными координатами. На всякий случай закомментирую расположение полярной системы координат: полюс совпадает с началом прямоугольной системы, а полярная ось – с положительным направлением оси
, однако по условию нужно воспользоваться полярными координатами. На всякий случай закомментирую расположение полярной системы координат: полюс совпадает с началом прямоугольной системы, а полярная ось – с положительным направлением оси ![]() . Полярную ось можно прочертить жирнее, но лично я часто этим пренебрегаю.
. Полярную ось можно прочертить жирнее, но лично я часто этим пренебрегаю.
При переходе к полярной системе координат произведение дифференциалов ВСЕГДА превращается в следующую вещь:
![]()
То есть, от интегрирования по декартовым «иксу» и «игреку» мы перешли к интегрированию по полярному радиусу «эр» и полярному углу «фи». Обратите внимание на дополнительно появившийся множитель ![]() , образно говоря, это «плата за переход», любители высшей математики могут погуглить якобиан перехода к полярным координатам. Практическая же сторона вопроса состоит в том, что этот множитель «эр» терять нельзя.
, образно говоря, это «плата за переход», любители высшей математики могут погуглить якобиан перехода к полярным координатам. Практическая же сторона вопроса состоит в том, что этот множитель «эр» терять нельзя.
Таким образом: ![]()
Но это ещё не всё – ведь границы области ![]() тоже заданы в декартовой системе. Используем формулы перехода к полярным координатам
тоже заданы в декартовой системе. Используем формулы перехода к полярным координатам ![]() . Ось ординат не трогаем, а вот окружность потревожим:
. Ось ординат не трогаем, а вот окружность потревожим:

![]() – получено типовое уравнение, на котором заострялось внимание ещё в статье Полярные координаты.
– получено типовое уравнение, на котором заострялось внимание ещё в статье Полярные координаты.
Теперь двойной интеграл ![]() необходимо свести к повторным интегралам. Для этого нужно выяснить порядок обхода области. На уроке Двойные интегралы для чайников мы орудовали виртуальной лазерной указкой, в полярных же координатах более удачна другая ассоциация – просвечивание области
необходимо свести к повторным интегралам. Для этого нужно выяснить порядок обхода области. На уроке Двойные интегралы для чайников мы орудовали виртуальной лазерной указкой, в полярных же координатах более удачна другая ассоциация – просвечивание области ![]() радаром. Представьте, что из точки полюса исходит луч света и вращается против часовой стрелки.
радаром. Представьте, что из точки полюса исходит луч света и вращается против часовой стрелки.
Когда луч радара поворачивается от полярной оси ![]() до угла
до угла ![]() (зелёная стрелка), то он входит в область
(зелёная стрелка), то он входит в область ![]() непосредственно из полюса (начиная со значения
непосредственно из полюса (начиная со значения ![]() ) и выходит из неё через окружность
) и выходит из неё через окружность ![]() (красная стрелка). Таким образом, на промежутке
(красная стрелка). Таким образом, на промежутке ![]() полярный радиус изменяется в пределах
полярный радиус изменяется в пределах ![]() , и область интегрирования полностью «просканирована».
, и область интегрирования полностью «просканирована».
В результате: 
Множитель ![]() , разумеется, уходит во внутренний интеграл, где осуществляется интегрирование по «эр».
, разумеется, уходит во внутренний интеграл, где осуществляется интегрирование по «эр».
Начинающим вновь рекомендую оформить концовку в два пункта:
1)  , чтобы продемонстрировать на следующем шаге примечательный факт, дальше упрощать пока не буду.
, чтобы продемонстрировать на следующем шаге примечательный факт, дальше упрощать пока не буду.
2) Подставляем трофей во внешний интеграл:
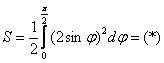
Заметьте, что здесь прорисовалась знакомая формула площади криволинейного сектора 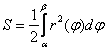 , которой мы активно пользовались на уроке Вычисление площади в полярных координатах с помощью интеграла, и фактически 2-й пункт – это повторение пройденного материала!
, которой мы активно пользовались на уроке Вычисление площади в полярных координатах с помощью интеграла, и фактически 2-й пункт – это повторение пройденного материала!
Используем формулу понижения степени:
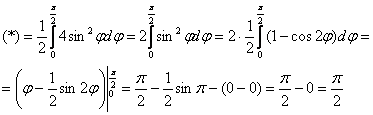
Что и требовалось получить.
Ответ: ![]()
В простых случаях, как этот, вычисления можно оформить и одной строкой:

Но злоупотреблять короткой дорожкой не советую – повышается риск запутаться.
В разобранной задаче жёстко требовалось использовать полярную систему координат, и это очень хорошо! Я не иронизирую. Как ни странно, более свободная формулировка условия может здОрово осложнить жизнь. Отрубим ящерице хвост:
«Вычислить площадь плоской фигуры, ограниченную линиями ![]() , с помощью двойного интеграла»
, с помощью двойного интеграла»
Дело в том, что площадь данной фигуры рассчитывается и с помощью двойного интеграла ![]() в прямоугольной системе координат. Но решение получается длительным и громоздим (см. задачу нахождения площади круга), и если человек не знает о возможности перехода к полярным координатам (а по условию это не запрещено!), то будет загружен трудной работой.
в прямоугольной системе координат. Но решение получается длительным и громоздим (см. задачу нахождения площади круга), и если человек не знает о возможности перехода к полярным координатам (а по условию это не запрещено!), то будет загружен трудной работой.
Давайте ещё укоротим условие:
«Вычислить площадь плоской фигуры, ограниченную линиями ![]() »
»
Здесь появилась новая степень свободы, и площадь фигуры помимо прочих способов можно рассчитать с помощью однократного интеграла (решение будет почти совпадать с решением через двойной интеграл). А люди со своеобразным чувством юмора вычислят площадь и по школьной формуле, чтобы затем настойчиво доказывать рецензенту корректность своего решения =) В чём, кстати, будут правы – ибо поборник конкретики должен и задачи ставить конкретно!
Чуть позже я коснусь ещё одной важной разновидности условия, а пока рассмотрим более содержательное задание:
Пример 2
С помощью двойного интеграла вычислить площадь фигуры, ограниченной линиями ![]() .
.
Решение: Изобразим данную фигуру на чертеже. С прямыми ![]() всё понятно, осталось прояснить вид линий 2-го порядка. Выделяем полные квадраты:
всё понятно, осталось прояснить вид линий 2-го порядка. Выделяем полные квадраты:
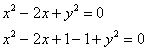
![]() – окружность единичного радиуса с центром в точке
– окружность единичного радиуса с центром в точке ![]() .
.

![]() – окружность с центром в точке
– окружность с центром в точке ![]() радиуса 2.
радиуса 2.
Таким образом:
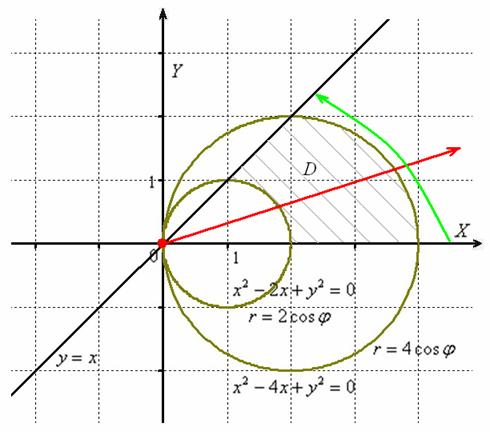
В условии задачи ничего не сказано о полярной системе координат, и поэтому площадь фигуры можно рассчитать «обычным» двойным интегралом. Но что-то не хочется. Впрочем, если найдётся энтузиаст и отправит мне разборчивое решение, то я его, пожалуй, опубликую в качестве страшилки =) ...И это случилось! Причём, двумя способами; первый демонстрирует, что бывает, когда не переходишь к новым пределам интегрирования в определённом интеграле. Таким образом, страшилка превзошла все ожидания. Спасибо за ваши письма! И возвращаемся к теме:
Какова предпосылка для перехода к полярным координатам?
Очевидно, что основной предпосылкой является наличие окружности (ей). Подчёркиваю, что это лишь предпосылка, а не обязательное правило! То есть, область интегрирования может быть ограничена окружностью (ями), но переход к полярным координатам только усложнит решение, а то и вообще заведёт его в тупик. И такие примеры встречаются реально.
Итак, площадь фигуры вычислим с помощью двойного интеграла, используя полярную систему координат:
![]()
По формулам перехода ![]() найдём полярные уравнения окружностей:
найдём полярные уравнения окружностей:

Теперь выясним порядок обхода области. Луч радара входит в область через окружность ![]() и выходит из неё через окружность
и выходит из неё через окружность ![]() (красная стрелка), при этом он осуществляет поворот от полярной оси
(красная стрелка), при этом он осуществляет поворот от полярной оси ![]() до угла
до угла ![]() (зелёная стрелка).
(зелёная стрелка).
Напомню также, что «альфа» и «бета» – это не просто формальные значения углов: полярное уравнение ![]() непосредственно задаёт полярную ось (положительное направление оси абсцисс), а уравнение
непосредственно задаёт полярную ось (положительное направление оси абсцисс), а уравнение ![]() – луч, исходящий из полюса и совпадающий с верхней частью прямой
– луч, исходящий из полюса и совпадающий с верхней частью прямой ![]() .
.
Примечание: если рассматривать обобщенные полярные координаты, то уравнение ![]() определяет полярную ось и её продолжение (всю ось абсцисс), а уравнение
определяет полярную ось и её продолжение (всю ось абсцисс), а уравнение ![]() – всю прямую
– всю прямую ![]()
В рассматриваемой задаче дана «хорошая» прямая ![]() и значение угла
и значение угла ![]() понятно «с ходу». Как найти угол в общем случае? Из материалов статьи Прямая на плоскости вспоминаем, что угловой коэффициент прямой
понятно «с ходу». Как найти угол в общем случае? Из материалов статьи Прямая на плоскости вспоминаем, что угловой коэффициент прямой ![]() равен тангенсу угла наклона данной прямой к положительному направлению оси абсцисс:
равен тангенсу угла наклона данной прямой к положительному направлению оси абсцисс: ![]() . В данном случае
. В данном случае ![]() , откуда следует, что
, откуда следует, что ![]() (если тяжко с числами – тригонометрические таблицы в помощь).
(если тяжко с числами – тригонометрические таблицы в помощь).
Возвращаемся к решению. По результатам «сканирования» области мы выяснили, что на промежутке ![]() полярный радиус изменяется в пределах
полярный радиус изменяется в пределах ![]() .
.
Перейдём к повторным интегралам:
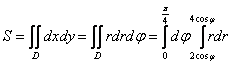
Остальное – дело техники:
1)
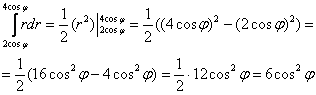
2)

Ответ: ![]()
Прикинув по чертежу количество клеточек, приходим к выводу, что полученный результат вполне и вполне правдоподобен.
Следующие два примера для самостоятельного решения:
Пример 3
С помощью двойного интеграла вычислить площадь фигуры, ограниченной линиями ![]()
Пример 4
Вычислить двойной интеграл, используя полярные координаты
![]()
В примере № 4 мы встретили ещё одну распространённую формулировку условия, в которой предложено непосредственно вычислить двойной интеграл. Да, он численно равен площади области ![]() , но, коль скоро, о площади изначально молчок, то и в решении об этом не нужно упоминать ;-) Подумайте, как грамотно записать ответ задания.
, но, коль скоро, о площади изначально молчок, то и в решении об этом не нужно упоминать ;-) Подумайте, как грамотно записать ответ задания.
Примерные образцы решений и чертежи в конце урока. Я их оформил в разном стиле, выбирайте, что больше нравится.
То были заезженные типовики, а сейчас на очереди более редкий, но очень интересный и поучительный экземпляр:
Пример 5
Вычислить двойной интеграл ![]()
Решение: определённый интеграл ![]() задаёт площадь области интегрирования, но о площади нас никто не спрашивал, поэтому никого не будем загружать своей эрудицией =) К тому же она сейчас ой как потребуется для других целей.
задаёт площадь области интегрирования, но о площади нас никто не спрашивал, поэтому никого не будем загружать своей эрудицией =) К тому же она сейчас ой как потребуется для других целей.
В чём заключается особенность этого задания? Прежде всего, бросается в глаза, что область «дэ» ограничена единственной кривой, и по характерным признакам – это какая-то алгебраическая линия 4-го порядка. Основная проблема у нас с чертежом. Конечно, можно погрузиться в справочники, но на это нет ни времени, ни особого желания. Поэтому мы попытаемся ограничиться общим анализом и обойтись совсем без чертежа.
Можно ли обойтись без чертежа?
Об этом я уже говорил на 1-м уроке: если условие задачи его не требует – то можно. Правда, область интегрирования всё равно придётся представить мысленно. Но даже если у вас есть такие способности, то демонстрировать их совсем не обязательно – потому что тяжелА жизнь вундеркинда =) И житейская мудрость заключается в том, что чертёжи, по возможности лучше выполнять. Однако у нас другой случай, когда наоборот – будет подозрительно смотреться построенный график линии 4-го порядка. Знаниями убивать тоже никого не надо, и в этой связи мы постараемся отделаться чисто аналитическим решением.
Поскольку область интегрирования, как правило, ограничена, то уравнение ![]() задаёт либо единственную замкнутую кривую, либо несколько ограниченных областей – что-то наподобие лепестков полярной розы. Ситуацию помогла бы прояснить область определения функции, но её нахождение тоже затруднено ввиду навороченности уравнения.
задаёт либо единственную замкнутую кривую, либо несколько ограниченных областей – что-то наподобие лепестков полярной розы. Ситуацию помогла бы прояснить область определения функции, но её нахождение тоже затруднено ввиду навороченности уравнения.
Что делать? Подумать о возможности использования полярной системы координат. Причём подумать самостоятельно – условие нам совершенно не намекает на способ решения. Поскольку в уравнении присутствуют знакомые «икс квадрат» и «игрек квадрат», то применение полярных координат действительно выглядит перспективно. По формулам перехода ![]() :
:
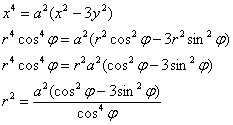
Вот и первое достижение – удалось понизить степень. С извлечением корня никаких шероховатостей, полярный радиус неотрицателен, параметр ![]() , косинус в знаменателе – в чётной степени:
, косинус в знаменателе – в чётной степени:
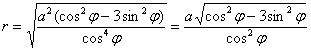
Теперь займёмся областью определения. Поскольку тригонометрические функции периодичны, то нас интересует промежуток ![]() , или, что то же самое
, или, что то же самое ![]() .
.
Знаменатель не может равняться нулю, поэтому ![]() .
.
Кроме того, подкоренное выражение должно быть неотрицательным: ![]() . Сведём данное условие к простейшему тригонометрическому неравенству, применив формулы понижения степени:
. Сведём данное условие к простейшему тригонометрическому неравенству, применив формулы понижения степени:
![]()
Таким образом:
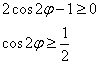
Я неоднократно ратовал за графическое решение подобных неравенств, но раз уж решили обойтись без чертежей, давайте вытащим из школьного учебника известную формулу. Решением неравенства ![]() , где
, где ![]() , является следующее множество промежутков:
, является следующее множество промежутков:
![]() , где
, где ![]() (любое целое число).
(любое целое число).
В нашем случае:

Разделим все части неравенства на 2:

В «сферу наших интересов» входят следующие значения «ка»:
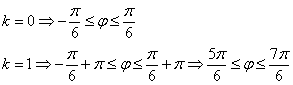
В результате, область определения полярной функции ![]() :
:

Два нижних значения не вошли в найденные выше промежутки, что избавляет нас от дополнительных хлопот. На отрезках ![]() расположены две одинаковые (в силу периодичности
расположены две одинаковые (в силу периодичности ![]() и
и ![]() ) кривые, и график функции
) кривые, и график функции ![]() , судя по всему, представляет собой что-то вроде двух одинаковых лепестков, как, собственно, и предполагалось.
, судя по всему, представляет собой что-то вроде двух одинаковых лепестков, как, собственно, и предполагалось.
Таким образом, достаточно рассмотреть промежуток ![]() , а результат удвоить. Луч радара, исходя из полюса
, а результат удвоить. Луч радара, исходя из полюса ![]() , сразу попадает в область интегрирования и выходит из неё через границу «лепестка»
, сразу попадает в область интегрирования и выходит из неё через границу «лепестка» ![]() ; при этом он осуществляет поворот от значения
; при этом он осуществляет поворот от значения ![]() до
до ![]() .
.
Переход к повторным интегралам, думаю, всем понятен:
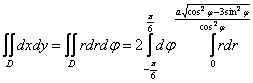
1) Понеслась нелёгкая:

2) Подставляем результат предыдущего пункта во внешний интеграл, не забывая про «двойку» перед ним (удвоение «лепестка»):

На первом шаге удвоили интеграл от чётной функции по симметричному относительно нуля отрезку. Чтобы «не таскать всё за собой», подынтегральную функцию удобно преобразовать отдельно. Приведём её к пригодному (и выгодному!) для интегрирования виду:

Если где-то возникли непонятки, посмотрите тригонометрические формулы. А если появились вопросы по самим принципам решения подобных интегралов, пожалуйста, посетите уроки Интегралы от тригонометрических функций и Сложные интегралы.
Завершаем вычисления:

Ответ: ![]()
Именно так. Не забываем, что в условии не спрашивалось о площадях и квадратных единицах. Однако после того как я нашёл в своих закромах этот трудный пример и включил его в содержание статьи, мне стало жутко интересно, так как же всё-таки выглядит график функции ![]() , и не допущена ли ошибка в вычислениях. Придав параметру значение
, и не допущена ли ошибка в вычислениях. Придав параметру значение ![]() , я изобразил график функции
, я изобразил график функции ![]() с помощью своего графопостроителя (см. Математические формулы и таблицы), и полученное значение площади
с помощью своего графопостроителя (см. Математические формулы и таблицы), и полученное значение площади ![]() оказалось очень похоже на правду. Желающие могут проделать то же самое. А если условие подобной задачи требует чертежа – то придётся =)
оказалось очень похоже на правду. Желающие могут проделать то же самое. А если условие подобной задачи требует чертежа – то придётся =)
Получился такой увлекательный разбор решения, что на этом фоне как-то затерялся тот момент, что в двойном интеграле ![]() может оказаться «настоящая» функция
может оказаться «настоящая» функция ![]() с «живым» «иксом» и/или «игреком»:
с «живым» «иксом» и/или «игреком»:
Пример 6
Вычислить двойной интеграл, используя полярные координаты
![]()
Решение: область интегрирования здесь очень простая – это часть кольца между концентрическими окружностями ![]() , которая располагается в четвёртой координатной четверти (о чём нам сообщают неравенства
, которая располагается в четвёртой координатной четверти (о чём нам сообщают неравенства ![]() ). И коль скоро так всё просто, можно сразу заняться переходом к полярной системе координат по формулам
). И коль скоро так всё просто, можно сразу заняться переходом к полярной системе координат по формулам ![]() .
.
Найдём уравнения окружностей:
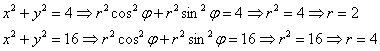
И выполним чертёж:
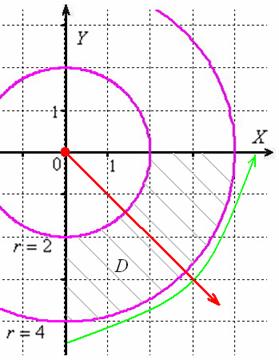
Порядок обхода области предельно понятен:

Можно было взять промежуток ![]() , но работать с табличным значением
, но работать с табличным значением ![]() гораздо привычнее.
гораздо привычнее.
Отличие от предыдущих примеров состоит в дополнительном шаге – преобразовании подынтегральной функции ![]() . Используем те же стандартные формулы перехода
. Используем те же стандартные формулы перехода ![]() . Если совсем просто, то в функцию двух переменных
. Если совсем просто, то в функцию двух переменных ![]() вместо «икс» подставляем
вместо «икс» подставляем ![]() и вместо «игрек»
и вместо «игрек» ![]() :
:
![]()
После подстановки максимально упрощаем выражение, но здесь этого особо не потребовалось.
Таким образом:

Фишка последнего шага должна быть вам хорошо знакома: когда проводится интегрирование по переменной «эр», то переменная «фи» считается константой (и наоборот). Поэтому константу ![]() целесообразно сразу вынести из внутреннего интеграла, чтобы она не мешалась под ногами.
целесообразно сразу вынести из внутреннего интеграла, чтобы она не мешалась под ногами.
Считаем:
1)
![]()
2)
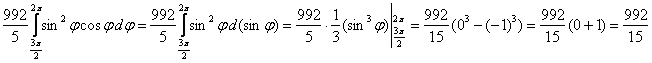
Ответ: ![]()
После того, как занавес опущен, повторим геометрический смысл полученного результата. По условию ![]() , следовательно,
, следовательно, ![]() , то есть поверхность, которую задаёт эта функция двух переменных, в 1-й и 4-й четвертях расположена над плоскостью
, то есть поверхность, которую задаёт эта функция двух переменных, в 1-й и 4-й четвертях расположена над плоскостью ![]() . Полученный в задаче результат – это в точности объём цилиндрического бруса, который ограничен плоскостью
. Полученный в задаче результат – это в точности объём цилиндрического бруса, который ограничен плоскостью ![]() снизу, поверхностью
снизу, поверхностью ![]() – сверху и множеством перпендикулярных плоскости
– сверху и множеством перпендикулярных плоскости ![]() прямых, проходящих через каждую точку границы области
прямых, проходящих через каждую точку границы области ![]() («четвертинки» кольца) – сбоку. Примерно 66 «кубиков»:
(«четвертинки» кольца) – сбоку. Примерно 66 «кубиков»: ![]() С задачей нахождения объёма тела мы вплотную столкнёмся при изучении тройных интегралов.
С задачей нахождения объёма тела мы вплотную столкнёмся при изучении тройных интегралов.
Завершим занятие несложным примером для самостоятельного решения:
Пример 7
Вычислить двойной интеграл, используя полярные координаты
![]()
Примерный образец чистового оформления задания в подвале.
Иногда область интегрирования приходится разбивать на две части и находить сумму двух двойных интегралов в полярных координатах, желающие могут потренироваться на Примерах № 8, 9 урока Площадь в полярных координатах. Кроме того, много дополнительных задач по теме можно раздобыть на странице готовых решений по высшей математике.
Желаю успехов!
Решения и ответы:
Пример 3: Решение: выделим полные квадраты и определим вид линий:

![]() – окружность единичного радиуса с центром в точке
– окружность единичного радиуса с центром в точке ![]() ;
;
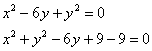
![]() – окружность единичного радиуса с центром в точке
– окружность единичного радиуса с центром в точке ![]() .
.
Изобразим область интегрирования на чертеже:
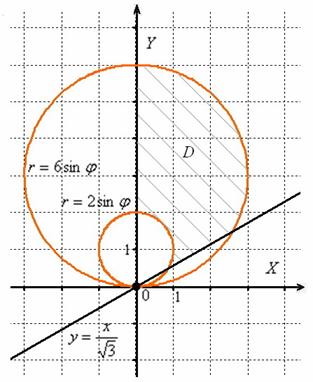
Площадь фигуры вычислим с помощью двойного интеграла, используя полярную систему координат:
Найдём угол наклона прямой ![]() :
:
![]()
Порядок обхода области:
Таким образом:

1)
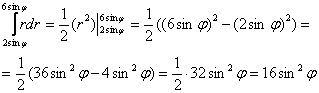
2)

Ответ: ![]()
Пример 4: Решение: найдём уравнения линий в полярной системе координат:
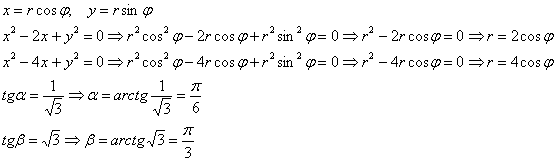
Изобразим область интегрирования на чертеже:
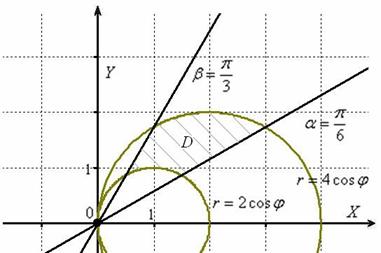
Порядок обхода области:

Таким образом: 
1)
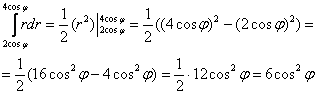
2)
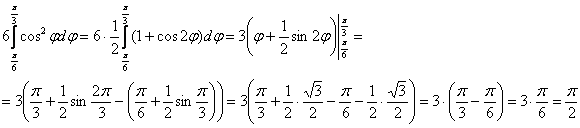
Ответ: ![]()
Пример 7: Решение: перейдём к полярной системе координат:

Изобразим область интегрирования на чертеже:
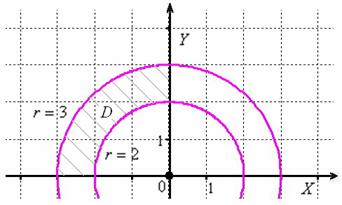
Порядок обхода области:
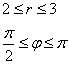
Таким образом:

1) ![]()
2)

Ответ: ![]()
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright