


Высшая математика – просто и доступно! 
 Вы находитесь на зеркале сайта mathprofi.ru
Вы находитесь на зеркале сайта mathprofi.ru
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Логарифмическая производная
Производные неявной, параметрической функций
Простейшие задачи
с производной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Дифференциальные уравнения в полных дифференциалах.
Примеры решений
Помимо дифференциальных уравнений с разделяющимися переменными, однородных уравнений и линейных неоднородных уравнений первого порядка, в практических задачах время от времени встречаются так называемые уравнения в полных дифференциалах. Да, конечно, ДУ в полных дифференциалах не такой частый гость в контрольных заданиях. Но освоить этот вид уравнений крайне важно, так как приёмы решения, о которых пойдет речь на данном уроке, потребуются при вычислении двойных, тройных, криволинейных интегралов, а также в ряде задач комплексного анализа.
Дифференциальные уравнения в полных дифференциалах – вещь довольно простая, вы даже удивитесь, насколько прозрачен и доступен алгоритм решения. Что необходимо знать, для того чтобы разобраться в этих диффурах? Во-первых, нужно ориентироваться в базовых понятиях темы, ответьте прямо сейчас на несколько простейших вопросов:
– Что такое дифференциальное уравнение?
– Что значит решить дифференциальное уравнение?
– Что такое общее решение, общий интеграл, частное решение?
В том случае, если возникло малейшее недопонимание терминов, или вы недавно столкнулись с диффурами и являетесь чайником, пожалуйста, начните с урока Дифференциальные уравнения первого порядка. Примеры решений. Согласитесь, плохо быть в неважной форме.
Во-вторых, необходимо уверенно находить частные производные. Всё будет крутиться вокруг них. Счастливые студенты, которые избежали плотного знакомства с частными производными на первом курсе, будут вынуждены добавить их в свои друзья, поскольку без навыков нахождения частных производных читать дальше просто нет смысла.
С любимых незабываемых частных производных и начнём.
Рассмотрим функцию двух переменных:
![]()
Такая вот простенькая функция.
Требуется найти частные производные первого порядка ![]() ,
, ![]() и составить полный дифференциал
и составить полный дифференциал ![]() .
.
В контексте данного урока я поменяю букву «зет» на букву «эф»:
Дана функция двух переменных ![]() . Требуется найти частные производные первого порядка
. Требуется найти частные производные первого порядка ![]() ,
, ![]() и составить полный дифференциал
и составить полный дифференциал ![]() .
.
Зачем потребовалась смена буквы? Традиционно сложилось, что в рассматриваемой теме в ходу буква ![]() . Кроме того, частные производные первого порядка будем чаще обозначать значками
. Кроме того, частные производные первого порядка будем чаще обозначать значками ![]() . Как мы помним из вводного урока про дифференциальные уравнения первого порядка, в диффурах «не в почёте» обозначать производную штрихом.
. Как мы помним из вводного урока про дифференциальные уравнения первого порядка, в диффурах «не в почёте» обозначать производную штрихом.
Решаем нашу короткую задачку.
Найдем частные производные первого порядка:
![]()
![]()
Полный дифференциал составим по формуле:
![]() , или, то же самое:
, или, то же самое: ![]()
В данном случае: ![]()
Пример 1
Решить дифференциальное уравнение ![]()
Не ожидали? =)
Но самое забавное, что уже известен ответ: ![]() , точнее, надо ещё добавить константу, получая общий интеграл
, точнее, надо ещё добавить константу, получая общий интеграл ![]() , который является решением дифференциального уравнения
, который является решением дифференциального уравнения ![]() .
.
Таким образом, дифференциальное уравнение ![]() имеет вид
имеет вид ![]() , то есть его левая часть является полным дифференциалом функции
, то есть его левая часть является полным дифференциалом функции ![]() . Отсюда и название – уравнение в полных дифференциалах.
. Отсюда и название – уравнение в полных дифференциалах.
Как решить диффур в полных дифференциалах? Очевидно, нужно выполнить некоторые обратные действия, чтобы восстановить исходную функцию ![]() и записать общий интеграл
и записать общий интеграл ![]() , который задаёт семейство функций одной независимой переменной («икс»). Не так давно я что-то там дифференцировал. Какое действие является обратным? Правильно, интегрирование. То есть речь пойдет о частном интегрировании, которое часто используется и в других задачах, упомянутых в начале урока.
, который задаёт семейство функций одной независимой переменной («икс»). Не так давно я что-то там дифференцировал. Какое действие является обратным? Правильно, интегрирование. То есть речь пойдет о частном интегрировании, которое часто используется и в других задачах, упомянутых в начале урока.
Рассмотрим алгоритм решения уравнения в полных дифференциалах
Итак, требуется решить дифференциальное уравнение:
![]()
Действие первое. Пожалуйста, забудьте задачку про частные производные и готовый ответ. Дело в том, что когда вам предложен для решения произвольный диффур, то вы ещё не знаете о том, что это уравнение в полных дифференциалах. И данный факт крайне желательно доказать в самом начале решения.
Докажем, что уравнение ![]() является уравнением в полных дифференциалах. Как это сделать? Уравнение в полных дифференциалах имеет вид
является уравнением в полных дифференциалах. Как это сделать? Уравнение в полных дифференциалах имеет вид ![]() . Вспоминаем характерное и очень удобное равенство смешанных производных второго порядка:
. Вспоминаем характерное и очень удобное равенство смешанных производных второго порядка: ![]() . Вот его и надо проверить:
. Вот его и надо проверить:
![]()
![]()
![]() , значит, данное уравнение является уравнением в полных дифференциалах.
, значит, данное уравнение является уравнением в полных дифференциалах.
На чистовике проверка проводится немного не так. Мы не имеем права использовать букву ![]() , так как изначально не знаем, является ли левая часть уравнения полным дифференциалом некоторой функции
, так как изначально не знаем, является ли левая часть уравнения полным дифференциалом некоторой функции ![]() . А вдруг не является? Тогда вышеприведенные записи с буквой
. А вдруг не является? Тогда вышеприведенные записи с буквой ![]() будут некорректны с математической точки зрения. Поэтому обычно используют нейтральные буквы «пэ» и «ку», а сама проверка на чистовике выглядит примерно так:
будут некорректны с математической точки зрения. Поэтому обычно используют нейтральные буквы «пэ» и «ку», а сама проверка на чистовике выглядит примерно так:
“
Проверим, является ли уравнение ![]() уравнением в полных дифференциалах:
уравнением в полных дифференциалах:
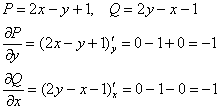
![]() , значит, данное ДУ является уравнением в полных дифференциалах
, значит, данное ДУ является уравнением в полных дифференциалах
”
Вот только теперь, после доказательства, мы можем использовать букву «эф», поскольку показано, что левая часть дифференциального уравнения ![]() является полным дифференциалом некоторой функции
является полным дифференциалом некоторой функции ![]() , и уравнение имеет вид:
, и уравнение имеет вид:
![]()
Ну, а коль скоро уравнение ![]() имеет вид
имеет вид ![]() , то:
, то:
![]()
![]()
Таким образом, нам известны две частные производные, и наша задача состоит в том, чтобы восстановить функцию ![]() и записать общий интеграл
и записать общий интеграл ![]() .
.
Существуют два зеркальных способа решения. В статье я остановлюсь на более привычном способе решения, но в конце рассмотрю и второй зеркальный вариант, он не менее важен.
Действие второе. Работаем с верхней производной ![]() . Нижнюю производную
. Нижнюю производную ![]() пока запишем на листочек и спрячем в карман.
пока запишем на листочек и спрячем в карман.
Если дана частная производная ![]() , то нужная нам функция
, то нужная нам функция ![]() восстанавливается с помощью обратного действия – частного интегрирования:
восстанавливается с помощью обратного действия – частного интегрирования:
![]()
Когда мы берём интеграл по «икс», то переменная «игрек» считается константой. Как видите, принцип точно такой же, как и при нахождении частных производных.
Я запишу подробно, сначала используем свойства линейности интеграла:
![]()
Еще раз подчеркиваю, что «игрек» в данном случае является константой и выносится за знак интеграла (т. е. не участвует в интегрировании).
В итоге:
![]()
Здесь ![]() – некоторая, пока ещё неизвестная функция, зависящая только от «игрек».
– некоторая, пока ещё неизвестная функция, зависящая только от «игрек».
Правильно ли вычислен интеграл? В этом легко убедиться, если выполнить проверку, т. е. найти частную производную:
![]() – получена исходная подынтегральная функция.
– получена исходная подынтегральная функция.
Надеюсь всем, понятно, почему ![]() . Функция
. Функция ![]() зависит только от «игрек», а, значит, является константой.
зависит только от «игрек», а, значит, является константой.
Действие третье.
Берем «недоделанный» результат ![]() и дифференцируем его по «игрек»:
и дифференцируем его по «игрек»:
![]()
Функцию ![]() мы пока не знаем, но производная-то по «игрек» у неё существует, поэтому запись
мы пока не знаем, но производная-то по «игрек» у неё существует, поэтому запись ![]() – совершенно законна.
– совершенно законна.
Действие четвертое.
Перепишем результат предыдущего пункта: ![]()
А теперь достаем из широких штанин листочек с производной:
![]()
Приравниваем:
![]()
и уничтожаем всё, что можно уничтожить:
![]()
Находим функцию ![]() , для этого нужно взять интеграл от правой части:
, для этого нужно взять интеграл от правой части:
![]()
Заключительный аккорд: подставим найденную функцию ![]() в «недоделанный» результат
в «недоделанный» результат ![]() :
:
![]() и приравняем полученную функцию к нулю, получая тем самым:
и приравняем полученную функцию к нулю, получая тем самым:
Ответ: общий интеграл: ![]()
Проверка уже выполнена в самом начале урока – находим частные производные функции ![]() , составляем полный дифференциал и приравниваем его к нулю. В результате должно получиться исходное дифференциальное уравнение.
, составляем полный дифференциал и приравниваем его к нулю. В результате должно получиться исходное дифференциальное уравнение.
Второй способ проверки состоит в том, чтобы найти производную неявно заданной функции, ведь общий интеграл – это неявные функции одной (независимой) переменной:

Кому как нравится, кому как удобнее, главное, о проверке не забывать!
Пример 2
Решить дифференциальное уравнение ![]()
Решение:
1) Проверим, является ли данное ДУ уравнением в полных дифференциалах:
![]()
! Не теряем минус при записи ![]() !
!
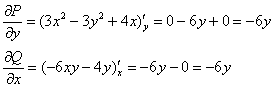
![]() , значит, уравнение
, значит, уравнение ![]() является уравнением в полных дифференциалах и имеет вид:
является уравнением в полных дифференциалах и имеет вид:
![]()
2) Запишем частные производные:
![]() – будем работать с этой производной.
– будем работать с этой производной.
![]() – про эту производную пока забываем.
– про эту производную пока забываем.
Если ![]() , то:
, то:

где ![]() – некоторая, пока ещё неизвестная функция, зависящая только от «игрек».
– некоторая, пока ещё неизвестная функция, зависящая только от «игрек».
Напоминаю, что, когда мы интегрируем по «икс», то переменная «игрек» считается константой и выносится за знак интеграла.
3) Берём «недоделанный» результат предыдущего пункта ![]() и дифференцируем его по «игрек»:
и дифференцируем его по «игрек»:
![]()
4) Переписываем найденный результат: ![]()
А теперь вспоминаем про «забытую» в начале второго пункта производную:
![]()
Приравниваем и упрощаем:
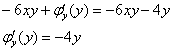
Примечание: на практике решение обычно записывают значительно короче, объединяя пункты № 3 и 4:
![]() , то есть сразу же после нахождения производной приравнивается «забытая» производная. В последнем равенстве
, то есть сразу же после нахождения производной приравнивается «забытая» производная. В последнем равенстве ![]() проводится взаимоуничтожение членов, откуда следует:
проводится взаимоуничтожение членов, откуда следует: ![]() .
.
Восстанавливаем функцию ![]() интегрированием по «игрек»:
интегрированием по «игрек»:
![]()
В «недоделанный» результат ![]() пункта № 2 подставляем найденную функцию
пункта № 2 подставляем найденную функцию ![]() и записываем
и записываем
ответ: общий интеграл: ![]()
Ответ можно записать и в стандартном виде ![]() , но здесь возникает любопытная особенность, о которой я рассказывал на уроке Дифференциальные уравнения первого порядка. Если мы переносим константу в правую часть, то, строго говоря, у неё следует сменить знак:
, но здесь возникает любопытная особенность, о которой я рассказывал на уроке Дифференциальные уравнения первого порядка. Если мы переносим константу в правую часть, то, строго говоря, у неё следует сменить знак: ![]() . Константу
. Константу ![]() (поскольку она может принимать любые значения) желательно переобозначить некоторой другой константой
(поскольку она может принимать любые значения) желательно переобозначить некоторой другой константой ![]() и записать общий интеграл в виде
и записать общий интеграл в виде ![]() . Если же записать ответ в виде
. Если же записать ответ в виде ![]() , то формально это будет ошибкой, а неформально – нет. Чтобы избежать лишних телодвижений с переобозначением константы или небрежности в оформлении, лично я предпочитаю оставлять ответ в виде
, то формально это будет ошибкой, а неформально – нет. Чтобы избежать лишних телодвижений с переобозначением константы или небрежности в оформлении, лично я предпочитаю оставлять ответ в виде ![]()
Выполним проверку. Найдём частные производные первого порядка:
![]()
![]()
Составим дифференциальное уравнение ![]() :
:
![]()
Получено исходное ДУ, значит, задание выполнено правильно.
Пример 3
Решить дифференциальное уравнение ![]()
Это пример для самостоятельного решения. Полное решение в конце урока я записал максимально коротко без пунктов, то есть приблизил его к «боевым» условиям – примерно так нужно оформлять задачу на практике.
Многочлены хорошо, а другие функции – лучше. Рассмотрим еще пару примеров.
Пример 4
Найти общий интеграл дифференциального уравнения.
![]()
Решение: проверим, является ли данное ДУ уравнением в полных дифференциалах:
![]() ,
, ![]()


![]() , значит, данное дифференциальное уравнение является уравнением в полных дифференциалах и имеет вид:
, значит, данное дифференциальное уравнение является уравнением в полных дифференциалах и имеет вид:
![]()
Запишем частные производные первого порядка:
![]() – работаем с этой производной
– работаем с этой производной
![]() – про эту производную пока забываем
– про эту производную пока забываем
Если ![]() , то:
, то:
![]()
Здесь ![]() является константой, которая вынесена за знак интеграла, а сам интеграл найден методом подведения функции под знак дифференциала.
является константой, которая вынесена за знак интеграла, а сам интеграл найден методом подведения функции под знак дифференциала.
Находим частную производную по «игрек»:
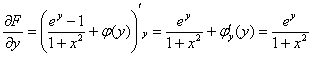
Это стандартное короткое оформление задания, когда после нахождения производной сразу приравнивается «забытая» производная ![]() .
.
Из последнего равенства ![]() следует, что
следует, что ![]() , и это простейший случай:
, и это простейший случай:
![]()
Подставляем найденную функцию ![]() в «недоделанный» результат
в «недоделанный» результат ![]()
Ответ: общий интеграл: ![]()
Пример 5
Найти общий интеграл дифференциального уравнения.

Это пример для самостоятельного решения, заодно проверите свои навыки в нахождении частных производных. Полное решение и ответ в конце урока.
А сейчас я рассмотрю обещанный зеркальный метод решения. Обязательно с ним ознакомьтесь, пригодится не только в диффурах, но и некоторых других задачах матана.
Пример 6
Найти общий интеграл дифференциального уравнения.

Начало решения точно такое же, необходимо убедиться, что перед нами уравнение в полных дифференциалах:
![]() ,
, ![]()


![]() , значит, данное дифференциальное уравнение является уравнением в полных дифференциалах и имеет вид:
, значит, данное дифференциальное уравнение является уравнением в полных дифференциалах и имеет вид:
![]()
![]() – про эту производную пока забываем.
– про эту производную пока забываем.
![]() – будем работать с этой производной.
– будем работать с этой производной.
Отличие состоит в том, что пляска начинается от другой производной. Может показаться, что второй способ «рассматривать не обязательно», но время от времени выручает именно он. Когда? Когда вы пытаетесь стандартно начать решение с верхней производной ![]() , но в результате получается очень трудный интеграл. В такой ситуации всегда следует попробовать начать решение с нижней производной
, но в результате получается очень трудный интеграл. В такой ситуации всегда следует попробовать начать решение с нижней производной ![]() , вполне возможно, что интеграл получится значительно проще.
, вполне возможно, что интеграл получится значительно проще.
Итак, если ![]() , то:
, то:

Восстановление функции ![]() проведено частным интегрированием по «игрек».
проведено частным интегрированием по «игрек».
Когда мы берём интеграл по «игрек», то переменная «икс» считается константой. Именно поэтому константа ![]() вынесена за знак интеграла и не принимает участия в интегрировании.
вынесена за знак интеграла и не принимает участия в интегрировании.
Функция ![]() зависит только от «икс» и пока ещё неизвестна.
зависит только от «икс» и пока ещё неизвестна.
Теперь находим частную производную по «икс»:
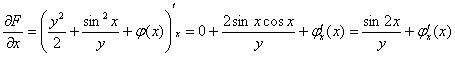
Вспоминаем о «забытой» производной: ![]()
Приравниваем результаты и проводим взаимоуничтожение дробей:
![]()
![]()
Функцию ![]() восстанавливаем интегрированием:
восстанавливаем интегрированием:
![]()
Добытый трофей ![]() подставляем в недостроенную функцию
подставляем в недостроенную функцию ![]() и записываем:
и записываем:
Ответ: общий интеграл: ![]()
Вторым способом можно было решить все примеры, которые мы рассмотрели до этого. Оба способа решения абсолютно равноценны, используйте тот, который вам удобнее.
Пример 7
Решить дифференциальное уравнение
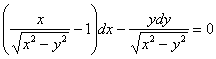
Это пример для самостоятельного решения. Решение в образце проведено вторым способом.
Заканчиваю печатать эту статью и обращаю внимание на то, что она получилась неожиданно большой. Когда материалы по диффурам в полных дифференциалах были только в моих планах, думал, урок получится меньше по объему раза в два. Что делать, присутствует новый материал – частное интегрирование. А новый материал в две строчки не уместишь.
Существуют еще так называемые уравнения, сводящиеся к уравнениям в полных дифференциалах. Они решаются методом интегрирующего множителя. В моей практике такие уравнения встречались, но всего 2-3 раза, и я не счел целесообразным включать их в методические материалы. Если возникнет необходимость рассмотреть метод интегрирующего множителя, пожалуйста, обратитесь к специализированной литературе по диффурам, в частности, можно воспользоваться решебником Обыкновенные дифференциальные уравнения, авторы – М.Л. Краснов, А.И. Киселёв, Г.И. Макаренко. Разберётесь легко, поскольку такое уравнение могут предложить только по причине хорошей успеваемости =)
Надеюсь, объяснения были достаточно подробны и понятны.
Полного вам дифференциала!
Решения и ответы:
Пример 3. Решение: ![]()
Проверим, является ли данное ДУ уравнением в полных дифференциалах:
![]()
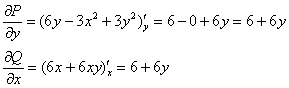
![]() , значит, данное уравнение является уравнением в полных дифференциалах:
, значит, данное уравнение является уравнением в полных дифференциалах:
![]()
Таким образом:
![]()
![]()
Если ![]() , то:
, то:
![]()
![]()

Ответ: общий интеграл: ![]()
Пример 5. Решение: проверим, является ли данное ДУ уравнением в полным дифференциалах:
![]() ,
, 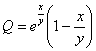
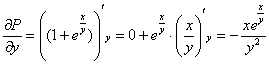
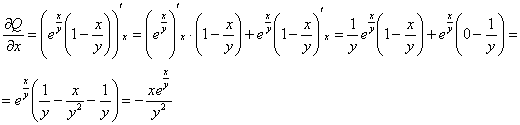
![]() , значит, данное ДУ является уравнением в полных дифференциалах и имеет вид:
, значит, данное ДУ является уравнением в полных дифференциалах и имеет вид:
![]()
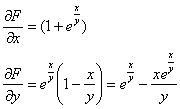
Если ![]() , то:
, то:
![]()
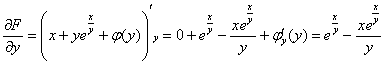
В последнем равенстве всё, как в мечте:
![]()
Ответ: общий интеграл: ![]()
Пример 7. Решение:
![]() ,
, ![]()
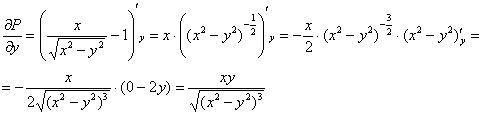

![]() , значит, данное ДУ является уравнением в полных дифференциалах и имеет вид:
, значит, данное ДУ является уравнением в полных дифференциалах и имеет вид:
![]()
![]()
![]()
Если ![]() , то:
, то:

Находим частную производную по «икс»:

Из последнего равенства ![]() после взаимоуничтожения дробей получаем:
после взаимоуничтожения дробей получаем:
![]()
Найдем ![]() :
:
![]()
Подставим найденную функцию ![]() в недостроенную функцию
в недостроенную функцию![]() .
.
Ответ: общий интеграл: ![]()
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright