Высшая математика – просто и доступно!

Вы находитесь на зеркале сайта mathprofi.ru

Наш форум, библиотека и блог: mathprofi.com

Высшая математика:

Математика для заочников

Математические формулы,
таблицы и другие материалы

Книги по математике

Математические сайты

+-*/^ Удобный калькулятор

+ «Дробовик»

Учимся решать:

Лекции-уроки по высшей математике для первого курса

Высшая математика для чайников, или с чего начать?
Повторяем школьный курс

Аналитическая геометрия:

Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида

Элементы высшей алгебры:

Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы

Пределы:

Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория

Производные функций:

Как найти производную?
Производная сложной функции. Примеры решений
Логарифмическая производная
Производные неявной, параметрической функций
Простейшие задачи
с производной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных

Функции и графики:

Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи

ФНП:

Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов

Интегралы:

Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Карта сайта

Лекции-уроки по высшей математике для второго курса

Дифференциальные уравнения:

Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты

Числовые ряды:

Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности

Функциональные ряды:

Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений

Кратные интегралы:

Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы

Элементы векторного анализа:

Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса

Комплексный анализ:

ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?

Теория вероятностей:

Математическая статистика:

Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Не нашлось нужной задачи?
Сборники готовых решений!

Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi

Обратная связь:

Часто задаваемые вопросы
Гостевая книга Отблагодарить автора >>>

Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом

Карта сайта

Как найти наибольшее и наименьшее значения функции
в ограниченной замкнутой области?

Близится к завершению изучение функций нескольких переменных, и сегодня мы рассмотрим ещё одну распространённую задачу, развёрнутую формулировку которой вы видите в заголовке статьи. Как многие догадываются, это пространственный аналог задачи нахождения наибольшего и наименьшего значений функции на отрезке, и для её решения потребуется минимальное знание темы. Заканчивается очередной учебный год, всем хочется на каникулы, и чтобы приблизить этот момент я сразу же перехожу к делу:

Начнём с области. Область, о которой идёт речь в условии, представляет собой ограниченное замкнутое множество точек плоскости . Например, множество точек, ограниченное треугольником, включая ВЕСЬ треугольник (если из границы «выколоть» хотя бы одну точку, то область перестанет быть замкнутой). На практике также встречаются области прямоугольной, круглой и чуть более сложных форм. Следует отметить, что в теории математического анализа даются строгие определения ограниченности, замкнутости, границы и т.д., но, думаю, все осознаЮт эти понятия на интуитивном уровне, а бОльшего сейчас и не надо.

Плоская область стандартно обозначается буквой , и, как правило, задаётся аналитически – несколькими уравнениями (не обязательно линейными); реже неравенствами. Типичный словесный оборот: «замкнутая область , ограниченная линиями ».

Неотъемлемой частью рассматриваемого задания является построение области на чертеже. Как это сделать? Нужно начертить все перечисленные линии (в данном случае 3 прямые) и проанализировать, что же получилось. Искомую область обычно слегка штрихуют, а её границу выделяют жирной линией:
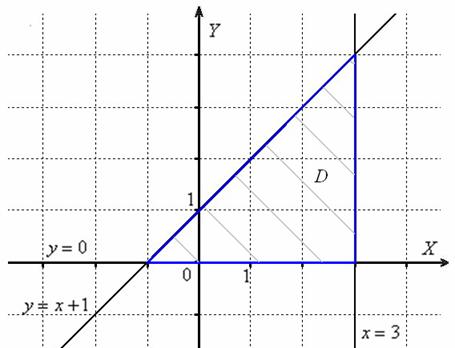
Плоская область обычно штрихуется, а её граница выделяется жирной либо цветной линией
Эту же область можно задать и линейными неравенствами: , которые почему-то чаще записывают перечислительным списком, а не системой.
Так как граница принадлежит области, то все неравенства, разумеется, нестрогие.

А теперь суть задачи. Представьте, что из начала координат прямо на вас выходит ось . Рассмотрим функцию , которая непрерывна в каждой точке области . График данной функции представляет собой некоторую поверхность, и маленькое счастье состоит в том, что для решения сегодняшней задачи нам совсем не обязательно знать, как эта поверхность выглядит. Она может располагаться выше, ниже, пересекать плоскость – всё это не важно. А важно следующее: согласно теоремам Вейерштрасса, непрерывная в ограниченной замкнутой области функция достигает в ней наибольшего (самого «высокого») и наименьшего (самого «низкого») значений, которые и требуется найти. Такие значения достигаются либо в стационарных точках, принадлежащих области D, либо в точках, которые лежат на границе этой области. Из чего следует простой и прозрачный алгоритм решения:

Пример 1

Найти наибольшее и наименьшее значения функции в ограниченной замкнутой области

Решение: прежде всего, нужно изобразить область на чертеже. К сожалению, мне технически трудно сделать интерактивную модель задачи, и поэтому я сразу приведу финальную иллюстрацию, на которой изображены все «подозрительные» точки , найденные в ходе исследования. Обычно они проставляются одна за другой по мере их обнаружения:
В процессе решения нужно отмечать найденные точки на чертеже

Исходя из преамбулы, решение удобно разбить на два пункта:

I) Найдём стационарные точки. Это стандартное действие, которые мы неоднократно выполняли на уроке об экстремумах нескольких переменных:

Найденная стационарная точка принадлежит области: (отмечаем её на чертеже), а значит, нам следует вычислить значение функции в данной точке:

– как и в статье Наибольшее и наименьшее значения функции на отрезке, важные результаты я буду выделять жирным шрифтом. В тетради их удобно обводить карандашом.

Обратите внимание на наше второе счастье – нет никакого смысла проверять достаточное условие экстремума. Почему? Даже если в точке функция достигает, например, локального минимума, то это ЕЩЁ НЕ ЗНАЧИТ, что полученное значение будет минимальным во всей области (см. начало урока о безусловных экстремумах).

Что делать, если стационарная точка НЕ принадлежит области? Почти ничего! Нужно отметить, что и перейти к следующему пункту.

II) Исследуем границу области.

Поскольку граница состоит из сторон треугольника, то исследование удобно разбить на 3 подпункта. Но лучше это сделать не абы как. С моей точки зрения, сначала выгоднее рассмотреть отрезки, параллельные координатным осям, и в первую очередь – лежащие на самих осях. Чтобы уловить всю последовательность и логику действий постарайтесь изучить концовку «на одном дыхании»:

1) Разберёмся с нижней стороной треугольника. Для этого подставим непосредственно в функцию:

Как вариант, можно оформить и так:

Геометрически это означает, что координатная плоскость (которая тоже задаётся уравнением ) «высекает» из поверхности «пространственную» параболу , вершина которой немедленно попадает под подозрение. Выясним, где она находится:

– полученное значение «попало» в область, и вполне может статься, что в точке (отмечаем на чертеже) функция достигает наибольшего либо наименьшего значения во всей области . Так или иначе, проводим вычисления:

Другие «кандидаты» – это, конечно же, концы отрезка. Вычислим значения функции в точках (отмечаем на чертеже):

Тут, кстати, можно выполнить устную мини-проверку по «урезанной» версии :

2) Для исследования правой стороны треугольника подставляем в функцию и «наводим там порядок»:

Здесь сразу же выполним черновую проверку, «прозванивая» уже обработанный конец отрезка:
, отлично.

Геометрическая ситуация родственна предыдущему пункту:

– полученное значение тоже «вошло в сферу наших интересов», а значит, нужно вычислить, чему равна функция в появившейся точке :

Исследуем второй конец отрезка :

Используя функцию , выполним контрольную проверку:

3) Наверное, все догадываются, как исследовать оставшуюся сторону . Подставляем в функцию и проводим упрощения:

Концы отрезка уже исследованы, но на черновике всё равно проверяем, правильно ли мы нашли функцию :
– совпало с результатом 1-го подпункта;
– совпало с результатом 2-го подпункта.

Осталось выяснить, если ли что-то интересное внутри отрезка :

– есть! Подставляя в уравнение прямой , получим ординату этой «интересности»:

Отмечаем на чертеже точку и находим соответствующее значение функции :

Проконтролируем вычисления по «бюджетной» версии :
, порядок.

И заключительный шаг: ВНИМАТЕЛЬНО просматриваем все «жирные» числа, начинающим рекомендую даже составить единый список:

из которого выбираем наибольшее и наименьшее значения. Ответ запишем в стилистике задачи нахождения наибольшего и наименьшего значений функции на отрезке:

На всякий случай ещё раз закомментирую геометрический смысл результата:
– здесь самая высокая точка поверхности в области ;
– здесь самая низкая точка поверхности в области .

В разобранной задаче у нас выявилось 7 «подозрительных» точек, но от задачи к задаче их количество варьируется. Для треугольной области минимальный «исследовательский набор» состоит из трёх точек. Такое бывает, когда функция , например, задаёт плоскость – совершенно понятно, что стационарные точки отсутствуют, и функция может достигать наибольшего/наименьшего значений только в вершинах треугольника. Но подобных примеров раз, два и обчёлся – обычно приходится иметь дело с какой-нибудь поверхностью 2-го порядка.

Если вы немного порешаете такие задания, то от треугольников голова может пойти кругом, и поэтому я приготовил для вас необычные примеры ~~чтобы она стала квадратной~~ :))

Пример 2

Найти наибольшее и наименьшее значения функции в замкнутой области, ограниченной линиями

Пример 3

Найти наибольшее и наименьшее значения функции в ограниченной замкнутой области .

Особое внимание обратите на рациональный порядок и технику исследования границы области, а также на цепочку промежуточных проверок, которая практически стопроцентно позволит избежать вычислительных ошибок. Вообще говоря, решать можно как угодно, но в некоторых задачах, например, в том же Примере 2, есть все шансы значительно усложнить себе жизнь. Примерный образец чистового оформления заданий в конце урока.

Систематизируем алгоритм решения, а то с моей прилежностью паука он как-то затерялся в длинной нити комментариев 1-го примера:

– На первом шаге строим область , её желательно заштриховать, а границу выделить жирной линией. В ходе решения будут появляться точки, которые нужно проставлять на чертеже.

– Найдём стационарные точки и вычислим значения функции только в тех из них, которые принадлежат области . Полученные значения выделяем в тексте (например, обводим карандашом). Если стационарная точка НЕ принадлежит области, то отмечаем этот факт значком либо словесно. Если же стационарных точек нет вовсе, то делаем письменный вывод о том, что они отсутствуют. В любом случае данный пункт пропускать нельзя!

– Исследуем границу области. Сначала выгодно разобраться с прямыми, которые параллельны координатным осям (если таковые есть вообще). Значения функции, вычисленные в «подозрительных» точках, также выделяем. О технике решения очень много сказано выше и ещё кое-что будет сказано ниже – читайте, перечитывайте, вникайте!

– Из выделенных чисел выбираем наибольшее и наименьшее значения и даём ответ. Иногда бывает, что такие значения функция достигает сразу в нескольких точках – в этом случае все эти точки следует отразить в ответе. Пусть, например, и оказалось, что это наименьшее значение. Тогда записываем, что

Заключительные примеры посвящены другим полезным идеям, которые пригодятся на практике:

Пример 4

Найти наибольшее и наименьшее значения функции в замкнутой области .

Я сохранил авторскую формулировку, в которой область задана в виде двойного неравенства. Это условие можно записать эквивалентной системой или же в более традиционном для данной задачи виде:

Напоминаю, что с нелинейными неравенствами мы сталкивались на самом первом уроке по теме ФНП, и если вам не понятен геометрический смысл записи , то, пожалуйста, не откладывайте и проясните ситуацию прямо сейчас ;-)

Решение, как всегда, начинается с построения области, которая представляет собой своеобразную «подошву»:
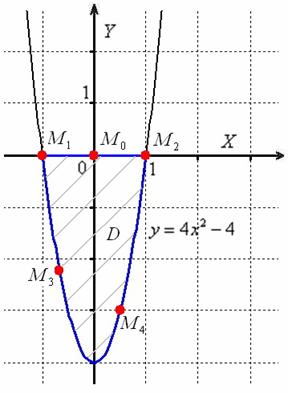
Область ограничена осью абсцисс и параболой

Мда, иногда приходится грызть не только гранит науки….

I) Найдём стационарные точки:

Система-мечта ~~идиота~~:)

Стационарная точка принадлежит области, а именно, лежит на её границе.

А так, оно, ничего… весело урок пошёл – вот что значит попить правильного чая =)

II) Исследуем границу области. Не мудрствуя лукаво, начнём с оси абсцисс:

1) Если , то

Найдём, где вершина параболы:
– ценИте такие моменты – «попали» прямо в точку , с которой уже всё ясно. Но о проверке всё равно не забываем:

Вычислим значения функции на концах отрезка:

2) С нижней частью «подошвы» разберёмся «за один присест» – безо всяких комплексов подставляем в функцию, причём, интересовать нас будет лишь отрезок :

Контроль:

Вот это уже вносит некоторое оживление в монотонную езду по накатанной колее. Найдём критические точки:

Решаем квадратное уравнение, помните ещё о таком? …Впрочем, помните, конечно, иначе бы не читали эти строки =) Если в двух предыдущих примерах были удобны вычисления в десятичных дробях (что, кстати, редкость), то здесь нас поджидают привычные обыкновенные дроби. Находим «иксовые» корни и по уравнению определяем соответствующие «игрековые» координаты точек-«кандидатов»:

Вычислим значения функции в найденных точках:

Проверку по функции проведите самостоятельно.

Теперь внимательно изучаем завоёванные трофеи и записываем ответ:

Вот это «кандидаты», так «кандидаты»!

Для самостоятельного решения:

Пример 5

Найти наименьшее и наибольшее значения функции в замкнутой области

Запись с фигурными скобками читается так: «множество точек , таких, что ».

Иногда в подобных примерах используют метод множителей Лагранжа, но реальная необходимость его применять вряд ли возникнет. Так, например, если дана функция с той же областью «дэ», то после подстановки в неё – с производной от никаких трудностей; причём оформляется всё «одной строкой» (со знаками ) без надобности рассматривать верхнюю и нижнюю полуокружности по отдельности. Но, конечно, бывают и более сложные случаи, где без функции Лагранжа (где , например, то же уравнение окружности) обойтись трудно – как трудно обойтись и без хорошего отдыха!

Всем хорошо сдать сессию и до скорых встреч в следующем сезоне!

Решения и ответы:

Пример 2: Решение: изобразим область на чертеже:

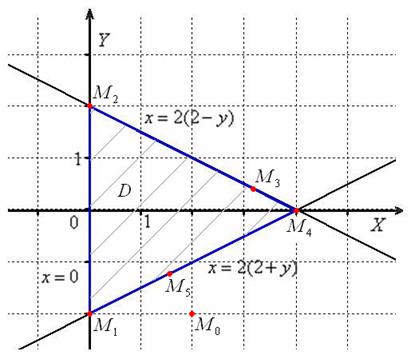
I) Вычислим значения функции в стационарных точках, принадлежащих данной области:

II) Исследуем границу области

1) Подставим в функцию:

Вычислим значение функции в точке :

Вычислим значение функции на другом конце отрезка:

2) Подставим в функцию :

Контроль:

Вычислим значение функции в точке :

Вычислим значение функции на конце отрезка:

3) Подставим в функцию :

Контроль:

Вычислим значение функции в точке :

Ответ:

Пример 3: Решение: изобразим область на чертеже:

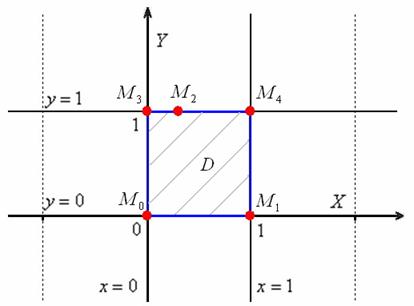
I) Вычислим значения функции в стационарных точках, принадлежащих данной области:

II) Исследуем границу области

1) Если , то
– точка уже исследована.
Вычислим значение функции на другом конце отрезка:

2) Если , то

Вычислим значение функции в точке :

Вычислим значения функции на концах отрезка:

3) Если , то
– точка уже исследована.
Другой конец отрезка также исследован.

4) Если , то

Концы отрезка уже исследованы.

Ответ:

Пример 5: Решение: изобразим область на чертеже:

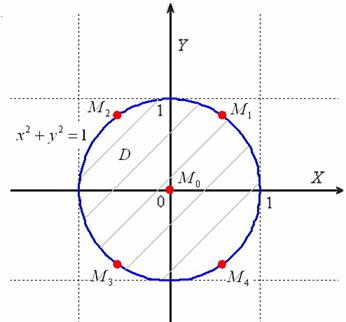
I) Найдём стационарные точки:

, следовательно, , – любое.
Таким образом, все точки оси – стационарные. Но область ограничена, и поэтому рассматриваем лишь точки из промежутка .

II) Исследуем границу области. Подставим в функцию (таким образом, учитываются сразу обе полуокружности ):

Найдём критические точки:

Если , то
Если , то
Вычислим значения функции в точках :