


Высшая математика – просто и доступно! 
 Вы находитесь на зеркале сайта mathprofi.ru
Вы находитесь на зеркале сайта mathprofi.ru
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Логарифмическая производная
Производные неявной, параметрической функций
Простейшие задачи
с производной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Интегрирование некоторых дробей.
Методы и приёмы решения
На данном уроке мы научимся находить интегралы от некоторых видов дробей. Для успешного усвоения материала Вам должны быть хорошо понятны выкладки статей Неопределенный интеграл. Примеры решений и Метод замены переменной в неопределенном интеграле.
Как я уже отмечал, в интегральном исчислении нет удобной формулы для интегрирования дроби 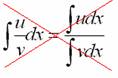 . И поэтому наблюдается грустная тенденция: чем «навороченнее» дробь, тем труднее найти от нее интеграл. В этой связи приходится прибегать к различным хитростям, о которых я сейчас и расскажу. Подготовленные читатели могут сразу воспользоваться оглавлением:
. И поэтому наблюдается грустная тенденция: чем «навороченнее» дробь, тем труднее найти от нее интеграл. В этой связи приходится прибегать к различным хитростям, о которых я сейчас и расскажу. Подготовленные читатели могут сразу воспользоваться оглавлением:
- Метод искусственного преобразования числителя
- Метод подведения под знак дифференциала для простейших дробей
- Метод выделения полного квадрата в знаменателе
- Подведение числителя под знак дифференциала
Метод искусственного преобразования числителя
Пример 1
Найти неопределенный интеграл. Выполнить проверку.
![]()
На уроке Неопределенный интеграл. Примеры решений мы избавлялись от произведения функций в подынтегральном выражении, превращая её в сумму, удобную для интегрирования. Оказывается, что иногда в сумму (разность) можно превратить и дробь!
Анализируя подынтегральную функцию, мы замечаем, что и в числителе и в знаменателе у нас находятся многочлены первой степени: ![]() и
и ![]() .
.
Когда в числителе и знаменателе находятся многочлены одинаковой степени, то помогает следующий искусственный приём: в числителе мы должны самостоятельно организовать такое же выражение, что и в знаменателе:
![]()
Рассуждение может быть следующим: «В числителе мне надо организовать ![]() , но если я прибавлю к «иксу» тройку, то, для того, чтобы выражение не изменилось – я обязан эту же тройку и вычесть».
, но если я прибавлю к «иксу» тройку, то, для того, чтобы выражение не изменилось – я обязан эту же тройку и вычесть».
Теперь можно почленно разделить числитель на знаменатель:
![]()
В результате мы добились, чего и хотели. Используем первые два правила интегрирования:

Готово. Проверку при желании выполните самостоятельно.
Обратите внимание, что ![]() во втором интеграле – это «халявная» сложная функция, об особенностях ее интегрирования я рассказал на уроке Метод замены переменной в неопределенном интеграле.
во втором интеграле – это «халявная» сложная функция, об особенностях ее интегрирования я рассказал на уроке Метод замены переменной в неопределенном интеграле.
Кстати, рассмотренный интеграл можно решить и методом замены переменной, обозначая ![]() , но запись решения получится значительно длиннее.
, но запись решения получится значительно длиннее.
Пример 2
Найти неопределенный интеграл. Выполнить проверку.
![]()
Это пример для самостоятельного решения. Следует заметить, что здесь метод замены переменной уже не пройдёт.
Внимание, важно! Примеры № 1, 2 являются типовыми и встречаются часто. В том числе, подобные интегралы нередко возникают в ходе решения других интегралов, в частности, при интегрировании иррациональных функций (корней).
Рассмотренный приём работает и в случае, если старшая степень числителя, больше старшей степени знаменателя.
Пример 3
Найти неопределенный интеграл. Выполнить проверку.
![]()
Начинаем подбирать числитель.
Алгоритм подбора числителя примерно такой:
1) В числителе мне нужно организовать ![]() , но там
, но там ![]() . Что делать? Заключаю
. Что делать? Заключаю ![]() в скобки и умножаю на
в скобки и умножаю на ![]() :
: ![]() .
.
2) Теперь пробую раскрыть эти скобки, что получится? ![]() . Хмм… уже лучше, но никакой двойки при
. Хмм… уже лучше, но никакой двойки при ![]() изначально в числителе нет. Что делать? Нужно домножить на
изначально в числителе нет. Что делать? Нужно домножить на ![]() :
:
![]()
3) Снова раскрываю скобки: ![]() . А вот и первый успех! Нужный
. А вот и первый успех! Нужный ![]() получился! Но проблема в том, что появилось лишнее слагаемое
получился! Но проблема в том, что появилось лишнее слагаемое ![]() . Что делать? Чтобы выражение не изменилось, я обязан прибавить к своей конструкции это же
. Что делать? Чтобы выражение не изменилось, я обязан прибавить к своей конструкции это же ![]() :
:
![]() . Жить стало легче. А нельзя ли еще раз в числителе организовать
. Жить стало легче. А нельзя ли еще раз в числителе организовать ![]() ?
?
4) Можно. Пробуем: ![]() . Раскрываем скобки второго слагаемого:
. Раскрываем скобки второго слагаемого:
![]() . Простите, но у меня вообще-то было на предыдущем шаге
. Простите, но у меня вообще-то было на предыдущем шаге ![]() , а не
, а не ![]() . Что делать? Нужно домножить второе слагаемое на
. Что делать? Нужно домножить второе слагаемое на ![]() :
:
![]()
5) Снова для проверки раскрываю скобки во втором слагаемом:
![]() . Вот теперь нормально: получено
. Вот теперь нормально: получено ![]() из окончательной конструкции пункта 3! Но опять есть маленькое «но», появилось лишнее слагаемое
из окончательной конструкции пункта 3! Но опять есть маленькое «но», появилось лишнее слагаемое ![]() , значит, я обязан прибавить к своему выражению
, значит, я обязан прибавить к своему выражению ![]() :
:
![]()
Если всё выполнено правильно, то при раскрытии всех скобок у нас должен получиться исходный числитель подынтегральной функции. Проверяем:
![]() Гуд.
Гуд.
Таким образом:

Готово. В последнем слагаемом я применил метод подведения функции под дифференциал.
Если найти производную от ответа и привести выражение к общему знаменателю, то у нас получится в точности исходная подынтегральная функция ![]() . Рассмотренный метод разложения
. Рассмотренный метод разложения ![]() в сумму – есть не что иное, как обратное действие к приведению выражения к общему знаменателю.
в сумму – есть не что иное, как обратное действие к приведению выражения к общему знаменателю.
Алгоритм подбора числителя в подобных примерах лучше выполнять на черновике. При некоторых навыках будет получаться и мысленно. Припоминаю рекордный случай, когда я выполнял подбор для 11-й степени, и разложение числителя заняло почти две строчки Вёрда.
Помимо алгоритма подбора можно использовать деление столбиком многочлена на многочлен, эта техника рассмотрена в статье Сложные пределы, а также на следующем уроке – Интегрирование дробно-рациональной функции.
Пример 4
Найти неопределенный интеграл. Выполнить проверку.
![]()
Это пример для самостоятельного решения.
Метод подведения под знак дифференциала для простейших дробей
Переходим к рассмотрению следующего типа дробей.
![]() ,
, ![]() ,
, ![]() ,
, ![]() (коэффициенты
(коэффициенты ![]() и
и ![]() не равны нулю).
не равны нулю).
На самом деле пара случаев с арксинусом и арктангенсом уже проскальзывала на уроке Метод замены переменной в неопределенном интеграле. Решаются такие примеры способом подведения функции под знак дифференциала и дальнейшим интегрированием с помощью таблицы. Вот еще типовые примеры с длинным и высоким логарифмом:
Пример 5
![]()
Пример 6
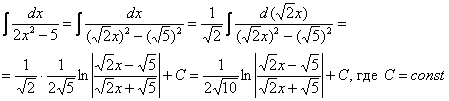
Тут целесообразно взять в руки таблицу интегралов и проследить, по каким формулам и как осуществляется превращение. Обратите внимание, как и зачем выделяются квадраты в данных примерах. В частности, в примере 6 сначала нужно представить знаменатель ![]() в виде
в виде ![]() , потом подвести
, потом подвести ![]() под знак дифференциала. А сделать это всё следует для того, чтобы воспользоваться стандартной табличной формулой
под знак дифференциала. А сделать это всё следует для того, чтобы воспользоваться стандартной табличной формулой ![]() .
.
Да что смотреть, попробуйте самостоятельно решить примеры № 7, 8, тем более, они достаточно короткие:
Пример 7
Найти неопределенный интеграл:
![]()
Пример 8
Найти неопределенный интеграл:
![]()
Если Вам удастся выполнить еще и проверку данных примеров, то большой респект – Ваши навыки дифференцирования на высоте.
Следует добавить, что такие интегралы можно решить и другим способом – с помощью выноса константы; один из читателей прислал своё решение Примера 7, полагая, что на сайте ошибка:

Но на самом деле получился эквивалентный ответ, к которому можно свести образец (см. в конце), с точностью до варьируемой константы.
Решайте, как нравится, однако в случае с «высоким» логарифмом (а-ка Примеры 6, 8) придётся повозиться с четырёхэтажными дробями.
Метод выделения полного квадрата
Интегралы вида ![]() ,
, ![]() (коэффициенты
(коэффициенты ![]() и
и ![]() не равны нулю) решаются методом выделения полного квадрата, который уже фигурировал на уроке Геометрические преобразования графиков.
не равны нулю) решаются методом выделения полного квадрата, который уже фигурировал на уроке Геометрические преобразования графиков.
На самом деле такие интегралы сводятся к одному из четырех табличных интегралов, которые мы только что рассмотрели. А достигается это с помощью знакомых формул сокращенного умножения:
![]() или
или ![]()
Формулы применяются именно в таком направлении, то есть, идея метода состоит в том, чтобы в знаменателе искусственно организовать выражения ![]() либо
либо ![]() , а затем преобразовать их соответственно в
, а затем преобразовать их соответственно в ![]() либо
либо ![]() .
.
Пример 9
Найти неопределенный интеграл
![]()
Это простейший пример, в котором при слагаемом ![]() – единичный коэффициент (а не какое-нибудь число или минус).
– единичный коэффициент (а не какое-нибудь число или минус).
Смотрим на знаменатель, здесь всё дело явно сведется к случаю ![]() . Начинаем преобразование знаменателя:
. Начинаем преобразование знаменателя:
![]()
Очевидно, что нужно прибавлять 4. И, чтобы выражение не изменилось – эту же четверку и вычитать:
![]()
Теперь можно применить формулу ![]() :
:
![]()
После того, как преобразование закончено ВСЕГДА желательно выполнить обратный ход: ![]() , всё нормально, ошибок нет.
, всё нормально, ошибок нет.
Чистовое оформление рассматриваемого примера должно выглядеть примерно так:
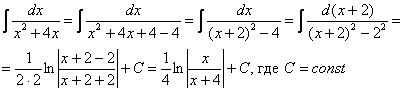
Готово. Подведением «халявной» сложной функции под знак дифференциала: ![]() , в принципе, можно было пренебречь
, в принципе, можно было пренебречь
Пример 10
Найти неопределенный интеграл:
![]()
Это пример для самостоятельного решения, ответ в конце урока
Пример 11
Найти неопределенный интеграл:
![]()
Что делать, когда перед ![]() находится минус? В этом случае, нужно вынести минус за скобки и расположить слагаемые в нужном нам порядке:
находится минус? В этом случае, нужно вынести минус за скобки и расположить слагаемые в нужном нам порядке: ![]() . Константу («двойку» в данном случае) не трогаем!
. Константу («двойку» в данном случае) не трогаем!
Теперь в скобках прибавляем единичку. Анализируя выражение, приходим к выводу, что и за скобкой нужно единичку – прибавить:
![]()
Тут получилась формула ![]() , применяем:
, применяем:
![]()
ВСЕГДА выполняем на черновике проверку:
![]() , что и требовалось проверить.
, что и требовалось проверить.
Чистовое оформление примера выглядит примерно так:

Усложняем задачу
Пример 12
Найти неопределенный интеграл:
![]()
Здесь при слагаемом ![]() уже не единичный коэффициент, а «пятёрка».
уже не единичный коэффициент, а «пятёрка».

(1) Если при ![]() находится константа, то её сразу выносим за скобки.
находится константа, то её сразу выносим за скобки.
(2) И вообще эту константу всегда лучше вынести за пределы интеграла, чтобы она не мешалась под ногами.
(3) Очевидно, что всё сведется к формуле ![]() . Надо разобраться в слагаемом
. Надо разобраться в слагаемом ![]() , а именно, получить «двойку»
, а именно, получить «двойку»
(4) Ага, ![]() . Значит, к выражению прибавляем
. Значит, к выражению прибавляем ![]() , и эту же дробь вычитаем.
, и эту же дробь вычитаем.
(5) Теперь выделяем полный квадрат. В общем случае также надо вычислить ![]() , но здесь у нас вырисовывается формула длинного логарифма
, но здесь у нас вырисовывается формула длинного логарифма ![]() , и действие
, и действие ![]() выполнять не имеет смысла, почему – станет ясно чуть ниже.
выполнять не имеет смысла, почему – станет ясно чуть ниже.
(6) Собственно, можно применить формулу ![]() , только вместо «икс» у нас
, только вместо «икс» у нас ![]() , что не отменяет справедливость табличного интеграла. Строго говоря, пропущен один шаг – перед интегрированием функцию
, что не отменяет справедливость табличного интеграла. Строго говоря, пропущен один шаг – перед интегрированием функцию ![]() следовало подвести под знак дифференциала:
следовало подвести под знак дифференциала: 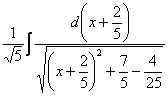 , но, как я уже неоднократно отмечал, этим часто пренебрегают.
, но, как я уже неоднократно отмечал, этим часто пренебрегают.
(7) В ответе под корнем желательно раскрыть все скобки обратно:
![]()
Сложно? Это еще не самое сложное в интегральном исчислении. Хотя, рассматриваемые примеры не столько сложны, сколько требуют хорошей техники вычислений.
Пример 13
Найти неопределенный интеграл:
![]()
Это пример для самостоятельного решения. Ответ в конце урока.
Существуют интегралы с корнями в знаменателе, которые с помощью замены сводятся к интегралам рассмотренного типа, о них можно прочитать в статье Сложные интегралы, но она рассчитана на весьма подготовленных студентов.
Подведение числителя под знак дифференциала
Это заключительная часть урока, тем не менее, интегралы такого типа встречаются довольно часто! Если накопилась усталость, может, оно, лучше завтра почитать? ;)
Интегралы, которые мы будем рассматривать, похожи на интегралы предыдущего параграфа, они имеют вид: ![]() или
или ![]() (коэффициенты
(коэффициенты ![]() ,
, ![]() и
и ![]() не равны нулю).
не равны нулю).
То есть, в числителе у нас появилась линейная функция. Как решать такие интегралы?
Пример 14
Найти неопределенный интеграл:
![]()
Пожалуйста, будьте внимательны, сейчас мы рассмотрим типовой алгоритм.
1) Когда дан интеграл вида ![]() или
или ![]() (коэффициенты
(коэффициенты ![]() ,
, ![]() и
и ![]() не равны нулю), то первое, что мы делаем, это… берём черновик. Дело в том, что сейчас нам предстоит выполнить небольшой подбор.
не равны нулю), то первое, что мы делаем, это… берём черновик. Дело в том, что сейчас нам предстоит выполнить небольшой подбор.
2) Заключаем выражение, которое находится в знаменателе (неважно – под корнем или без корня) под знак дифференциала, в данном примере: ![]()
3) Раскрываем дифференциал:
![]()
Смотрим на числитель нашего интеграла: ![]()
Немного разные вещи получились…. А теперь нам нужно подобрать множитель для дифференциала ![]() , такой, чтобы при его раскрытии получилось, как минимум,
, такой, чтобы при его раскрытии получилось, как минимум, ![]() . В данном случае подходящим множителем является:
. В данном случае подходящим множителем является: ![]()
4) Для самоконтроля снова раскрываем наш дифференциал:
![]()
Снова смотрим на числитель нашего интеграла: ![]() .
.
Уже ближе, но у нас не то слагаемое: ![]()
5) К нашему дифференциалу ![]() :
:
– приписываем слагаемое, которое у нас изначально было в подынтегральной функции:
![]()
– Вычитаем (в данном случае – вычитаем, иногда нужно, наоборот, прибавлять) наше «не то» слагаемое: ![]()
– Обе константы берем в скобки и приписываем справа значок дифференциала:
![]()
– Вычитаем (в некоторых примерах нужно сложить) константы:
![]()
6) Выполняем проверку:

У нас получился в точности числитель подынтегральной функции, значит, подбор выполнен успешно.
Чистовое оформление решения выглядит примерно так:

(1) Выполняем на черновике подбор числителя согласно вышерассмотренному алгоритму. Обязательно выполняем проверку, правильно ли выполнен подбор. При определенном опыте решения интегралов подбор нетрудно выполнить и в уме.
(2) Почленно делим числитель на знаменатель. В практическом решении задач данный шаг можно опускать
(3) Используя свойство линейности, разделяем интегралы. Все константы целесообразно вынести за знаки интегралов.
(4) Первый интеграл фактически является табличным, используем формулу ![]() (константу
(константу ![]() припишем позже, когда возьмем второй интеграл). Во втором интеграле выделяем полный квадрат (такой тип интегралов мы рассмотрели в предыдущем параграфе).
припишем позже, когда возьмем второй интеграл). Во втором интеграле выделяем полный квадрат (такой тип интегралов мы рассмотрели в предыдущем параграфе).
Остальное дело техники.
И, на закуску, пара примеров для самостоятельного решения – один проще, другой сложнее.
Пример 15
Найти неопределенный интеграл:
![]()
Пример 16
Найти неопределенный интеграл:
![]()
Для решения данных примеров будет полезен частный случай интегрирования степенной функции, которого нет в моей таблице: ![]()
Как видите, интегрирование дробей – дело кропотливое, часто приходится применять искусственные приемы и подборы. Но что делать…
Существуют и другие виды дробей, так называемые дробно-рациональные функции, они решаются методом неопределенных коэффициентов. Но это уже тема урока Интегрирование дробно рациональных функций.
Желаю успехов!
Решения и ответы:
Пример 2. Решение:
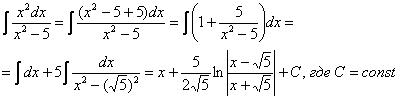
Пример 4. Решение:

Пример 7. Решение:
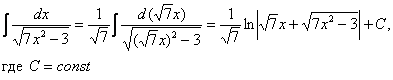
Пример 8:.Решение:
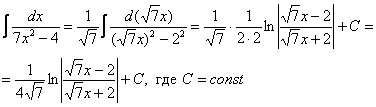
Пример 10. Решение:
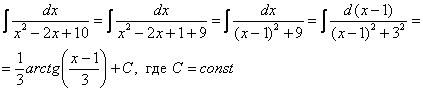
Пример 13. Решение:

Пример 15. Решение:
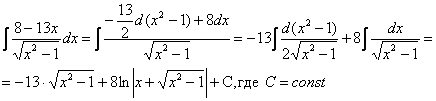
Пример 16. Решение:

Я проверил каждый пример, а Вы? ;)
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright