Высшая математика – просто и доступно!

Вы находитесь на зеркале сайта mathprofi.ru

Наш форум, библиотека и блог: mathprofi.com

Высшая математика:

Математика для заочников

Математические формулы,
таблицы и другие материалы

Книги по математике

Математические сайты

+-*/^ Удобный калькулятор

+ «Дробовик»   

Учимся решать:

  Карта сайта

Не нашлось нужной задачи?
Сборники готовых решений!

Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi

Обратная связь:

Часто задаваемые вопросы
Гостевая книга Отблагодарить автора >>>

Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом

Карта сайта

---

Приближенное вычисление определенного интеграла
с помощью разложения подынтегральной функции в ряд

Этот небольшой урок позволит не только освоить типовую задачу, которая довольно часто встречается на практике, но и закрепить материалы статьи Разложение функций в степенные ряды. Нам потребуется таблица разложений функций в степенные ряды, которую можно раздобыть на странице Математические формулы и таблицы. Кроме того, читатель должен понимать геометрический смысл определенного интеграла и обладать элементарными навыками интегрирования.

На уроке Определенный интеграл. Как вычислить площадь фигуры? речь шла о том, что определенный интеграл – это площадь. Но в некоторых случаях интеграл является очень трудным или неберущимся, поэтому соответствующую площадь в большинстве случаев можно вычислить только приближенно.

Например: вычислить определенный интеграл 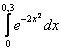. Такой интеграл является неберущимся, но аналитически и геометрически всё хорошо:

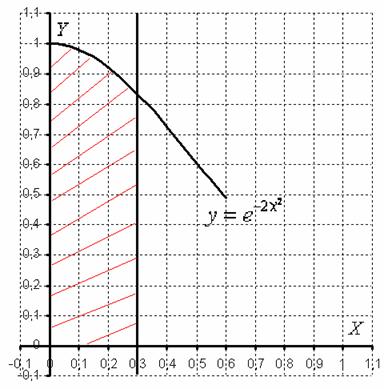
Мы видим, что подынтегральная функция непрерывна на отрезке , а значит, площадь существует, и определенный интеграл  численно равен заштрихованной площади. Беда только в том, что данную площадь можно вычислить лишь приближенно с определенной точностью. На основании вышеизложенных фактов и  появилась типовая задача курса высшей математики.

Пример 1

Вычислить приближенно определенный интеграл, предварительно разложив подынтегральную функцию в ряд Маклорена, с точностью до 0,001

Решение: Идея метода состоит в том, чтобы заменить подынтегральную функцию соответствующим степенным рядом (если он, конечно, сходится к ней на промежутке интегрирования).

Поэтому на первом этапе нужно разложить подынтегральную функцию в ряд Маклорена. Эту распространенную на практике задачу мы очень подробно рассмотрели на уроке Разложение функций в степенные ряды. Кстати, рекомендую всем прочитать, поскольку некоторые вещи, о которых сейчас пойдет разговор, могут показаться малопонятными.

Используем табличное разложение:

В данном случае

Обратите внимание, как я записал ряд. Специфика рассматриваемого задания требует записывать только несколько первых членов ряда. Мы не пишем общий член ряда , он здесь ни к чему.

Чем больше членов ряда мы рассматриваем – тем лучше будет точность. Сколько слагаемых рассматривать? Из практики могу сказать, что в большинстве случаев для достижения точности 0,001 достаточно записать первые 4 члена ряда. Иногда требуется меньше. А иногда больше. Если в практическом примере их не хватило, то придётся переписывать всё заново =( Поэтому целесообразно провести предварительный черновой анализ или перестраховаться, изначально записав побольше членов (собственно, такой же совет как и для приближенного вычисления значения функции с помощью ряда).

Следует также отметить, что точность до трёх знаков после запятой самая популярная. Также в ходу и другая точность вычислений, обычно 0,01 или 0,0001.

Теперь второй этап решения:
Сначала меняем подынтегральную функцию на полученный степенной ряд:

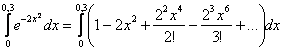
Почему это вообще можно сделать? Данный факт пояснялся ещё на уроке о разложении функций в степенные ряды – график бесконечного многочлена  в точности совпадает с графиком функции ! Причем, в данном случае утверждение справедливо для любого значения «икс», а не только для отрезка интегрования .

На следующем шаге максимально упрощаем каждое слагаемое:

Лучше это сделать сразу, чтобы на следующем шаге не путаться с лишними вычислениями.

После упрощений почленно интегрируем всю начинку – напоминаю, что эта замечательная возможность обусловлена равномерной сходимостью степенных рядов:

Интегралы здесь простейшие, на этом я не останавливаюсь.

На завершающем этапе вспоминаем школьную формулу Ньютона-Лейбница . Для тех, кто не смог устоять перед Ньютоном и Лейбницем, есть урок Определенные интегралы. Примеры решений.

Техника вычислений стандартна: сначала подставляем в каждое слагаемое 0,3, а затем ноль. Для вычислений используем калькулятор:

Сколько членов ряда нужно взять для окончательных вычислений?  Если сходящийся ряд знакочередуется, то абсолютная погрешность вычислений по модулю не превосходит последнего отброшенного члена ряда. В нашем случае уже третий член ряда меньше требуемой точности 0,001, и поэтому если мы его отбросим, то заведомо ошибёмся не более чем на 0,000972 (осознайте, почему!). Таким образом, для окончательного расчёта достаточно первых двух членов: .

Ответ: 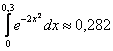, с точностью до 0,001

Что это получилось за число с геометрической точки зрения?   – это приблизительная площадь заштрихованной фигуры (см. рисунок выше).

Пример 2

Вычислить приближенно определенный интеграл, предварительно разложив подынтегральную функцию в ряд по степеням , с точностью до 0,001

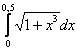
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.

Как-то незаслуженно я обошел стороной арктангенс, ни разу не разложив его в ряд. Исправим оплошность.

Пример 3

Вычислить определенный интеграл с точностью 0,01 с помощью разложения подынтегральной функции в ряд.

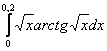
Решение: Есть сильное подозрение, что данный интеграл является берущимся, правда, решение не самое простое.

Разложим подынтегральную функцию в ряд Маклорена. Используем разложение:

В данном случае


Здесь повезло, что в итоге степени таки остались целыми, дробные степени было бы труднее интегрировать.

Таким образом:

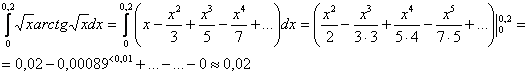
Бывает и так. Члены с возу – студенту легче.

Ответ:  с точностью до 0,01.

И снова обратите внимание, что точность 0,01 здесь гарантирована лишь потому, что сходящийся ряд знакочередуется. Для ряда с положительными членами, например, ряда  такую оценку проводить нельзя, поскольку сумма отброшенного «хвоста» может запросто превысить 0,00089. Что делать в таких случаях? Расскажу в конце урока. А пока открою секрет, что во всех сегодняшних примерах ряды знакочередуются.

И, конечно, следует контролировать область сходимости ряда. В рассмотренном примере она, кстати, «урезана»: (из-за квадратного корня), однако наш отрезок интегрирования полностью лежит в данной области.

Что произойдёт в «нелегальном» случае, например, с интегралом ? Функция так же прекрасно разложится в ряд, члены ряда так же замечательно проинтегрируются. Но, когда мы начнем подставлять значение верхнего предела  по формуле Ньютона-Лейбница, то увидим, что числа будут неограниченно расти, то есть каждое следующее число будет больше, чем предыдущее. Ряд-то сходится лишь на отрезке . Это не паранойя, на практике так время от времени бывает.

Что делать, если вам встретился подобный интеграл? Во-первых, имеет смысл проконсультировать с преподавателем – скорее всего, это опечатка в задачнике или методичке, где авторы недосмотрели, что промежуток интегрирования «вылез» за область сходимости ряда. А может и досмотрели (особенно, если вы учитесь углублённо). Дело в том, что на самом деле этот интеграл разрешим! Разбиваем его на две части:

Первый интеграл вычисляется штатно, а вот во втором – раскладываем функцию  в ряд Тейлора по степеням  с помощью производных (см. последний параграф), тогда область сходимости полученного ряда будет такова:

 – прибавляем ко всем частям неравенства единицу:
 – и далее преспокойно интегрируем ряд в его области сходимости!

Вот такая вот совсем не очевидная задача, выражаю благодарность одному из читателей, который указал на этот вариант развития событий.

Интеграл с арксинусом я рассматривать не буду, поскольку он занесен в красную книгу. Лучше дополнительно рассмотреть что-нибудь «бюджетное»:

Пример 4

Вычислить определенный интеграл с точностью 0,001 путем разложения подынтегральной функции в ряд и почленного интегрирования этого ряда.

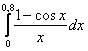
Это пример для самостоятельного решения. Что касаемо нуля, то он здесь не помеха – подынтегральная функция терпит лишь устранимый разрыв в точке , и поэтому несобственный интеграл здесь и рядом не валялся, т.е. речь идёт по-прежнему об определённом интеграле. В ходе решения вы увидите, что полученный ряд прекрасно сходится к нулю.

В заключение рассмотрим еще пару примеров, которые несколько сложнее.

Пример 5

Вычислить определенный интеграл с точностью 0,001 с помощью разложения подынтегральной функции в ряд и почленного интегрирования этого ряда.

Решение: Анализирую подынтегральную функцию, приходим к выводу, что нужно использовать биномиальное разложение. Но сначала функцию надо представить в соответствующем виде:

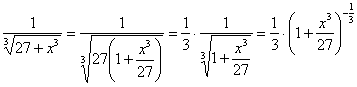
К сожалению, ни один частный случай биномиального разложения не подходит, и нам придется использовать громоздкую общую формулу:

В данном случае: ,

Разложение уже на этом этапе лучше максимально упростить. Замечаем также, что четвертый член ряда нам, очевидно, не потребуется, так как в нём еще до интегрирования появилась дробь , которая заведомо меньше требуемой точности 0,001.

Не забываем, что есть еще один множитель:

Наиболее кропотливый этап пройден, вычислим интеграл:

Ответ:  с точностью до 0,001.

Нечто подобное для самостоятельного  решения:

Пример 6

Вычислить определенный интеграл с точностью 0,001 путем разложения подынтегральной функции в ряд и почленного интегрирования этого ряда.

И напоследок обещанный секрет – что делать, если все члены ряда положительны? Скорее всего, в этом случае от вас не потребует вычислить интеграл «с точностью до», а попросят, например, найти сумму первых трёх членов ряда и опционально округлить её до скольких-то знаков после запятой. Но это будет вовсе не «с точностью до», т.к. для положительных рядов довольно трудно оценить сумму остатка. Однако, если «тяжёлый случай» таки имеет место, то обратитесь за консультацией к преподавателю; в рамках данной статьи я не буду освещать специальные методы, которые не находят широкого практического применения.

Рассмотренная типовая задача на самом деле довольно неприятна, так как не существует простых способов проверки результата. По невнимательности легко пропустить какое-нибудь число, степень, неточно разложить функцию в ряд, неверно проинтегрировать, допустить банальную ошибку в вычислениях. Поэтому очень важно подходить к решению таких задач с ясной головой.

Желаю успехов!

Решения и ответы:

Пример 2: Решение: разложим подынтегральную функцию в ряд.
Используем частный случай биномиального разложения: 

В данном случае:

Таким образом:

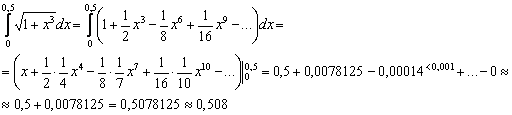
Ответ:  с точностью до 0,001.

Пример 4: Решение: разложим подынтегральную функцию в ряд.
Используем  разложение:   


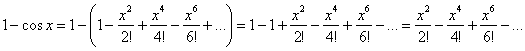
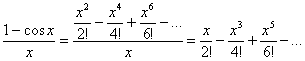
Таким образом:

Ответ: 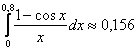 с точностью до 0,001.

Пример 6: Решение:

Используем биномиальное разложение:

В данном случае: , :

Таким образом:

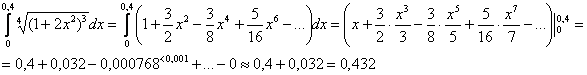
Ответ:  с точностью до 0,001.

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

Zaochnik.com – профессиональная помощь студентам,

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

© Copyright  Александр Емелин, mathprofi.ru, 2010-2024, сделано в Блокноте