


Высшая математика – просто и доступно! 
 Вы находитесь на зеркале сайта mathprofi.ru
Вы находитесь на зеркале сайта mathprofi.ru
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Логарифмическая производная
Производные неявной, параметрической функций
Простейшие задачи
с производной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Как привести уравнение линии второго порядка
к каноническому виду?
Задача приведения уравнения линии 2-го порядка к каноническому виду следовала за нами практически с самого начала изучения темы и сейчас мы окончательно разберёмся, как общее уравнение линии второго порядка ![]() (здесь и далее подразумевается, что
(здесь и далее подразумевается, что ![]() не равны одновременно нулю) свести к одному из девяти канонических случаев.
не равны одновременно нулю) свести к одному из девяти канонических случаев.
В статьях об эллипсе, гиперболе и параболе, а также на практикуме Задачи с линиями второго порядка очень подробно отработан частный случай уравнения, когда коэффициент ![]() :
:
![]()
Пожалуйста, внимательно посмотрите на своё уравнение, которое вам нужно привести к каноническому виду – есть ли в нём слагаемое, которое содержит произведение ![]() ?
?
Если такого слагаемого нет, то вам хватит материалов перечисленных выше уроков.
Если же такое слагаемое есть – то не хватит =)
Как многие подметили, члены ![]() общего уравнения «отвечают» за параллельный перенос линии, который имеет место, когда хотя бы один из коэффициентов
общего уравнения «отвечают» за параллельный перенос линии, который имеет место, когда хотя бы один из коэффициентов ![]() отличен от нуля. И логично предположить, что ненулевое слагаемое
отличен от нуля. И логично предположить, что ненулевое слагаемое ![]() «отвечает» за поворот линии. Исключение составляет угол в 90 градусов (а также любой кратный ему угол, например
«отвечает» за поворот линии. Исключение составляет угол в 90 градусов (а также любой кратный ему угол, например ![]() ), при повороте на который мы отделываемся лёгким испугом, укладываясь в рамки хорошо отшлифованного частного случая
), при повороте на который мы отделываемся лёгким испугом, укладываясь в рамки хорошо отшлифованного частного случая ![]() . Простейший пример поворота на «нехороший» угол нам уже встречался – это неканонически расположенная «школьная» гипербола
. Простейший пример поворота на «нехороший» угол нам уже встречался – это неканонически расположенная «школьная» гипербола ![]() (см. Пример 5 статьи Гипербола и парабола).
(см. Пример 5 статьи Гипербола и парабола).
Уравнение ![]() с ненулевым коэффициентом «бэ» неприятно тем, что в общем случае его невозможно привести к каноническому виду с помощью обычных средств алгебры: переноса слагаемых, их группировки, вынесений за скобки, выделения полных квадратов и прочей школьной самодеятельности. Поэтому на помощь приходится привлекать более мощные методы решения.
с ненулевым коэффициентом «бэ» неприятно тем, что в общем случае его невозможно привести к каноническому виду с помощью обычных средств алгебры: переноса слагаемых, их группировки, вынесений за скобки, выделения полных квадратов и прочей школьной самодеятельности. Поэтому на помощь приходится привлекать более мощные методы решения.
Рассмотрим в качестве примера уравнение ![]() . Какие будут идеи? …Да ладно с ними, с идеями, тут даже не понятно, какую линию оно задаёт. Эллипс? Гиперболу? Параболу? Что-то другое из классификации?
. Какие будут идеи? …Да ладно с ними, с идеями, тут даже не понятно, какую линию оно задаёт. Эллипс? Гиперболу? Параболу? Что-то другое из классификации?
Немного потраченного времени, и вы научитесь довольно легко находить ответы на эти вопросы, в частности, без особых проблем сможете определить, что данное уравнение определяет эллипс с полуосями ![]() , который расположен центром в точке
, который расположен центром в точке ![]() и повёрнут относительного своего канонического положения на отрицательный угол, составляющий примерно
и повёрнут относительного своего канонического положения на отрицательный угол, составляющий примерно ![]() :
:
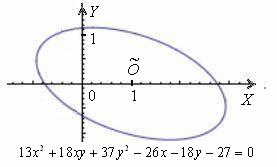
Мысленно возьмите эллипс в руки, поверните его на любой угол и переместите в произвольное место плоскости. Новому положению эллипса будет соответствовать совершенно другое уравнение, и если вам предъявить его без чертежа, то никто в жизнь не догадается, что оно определяет тот же самый эллипс. Именно поэтому и появилась задача приведения уравнения к каноническому виду – чтобы независимо от расположения линии выяснить, что это за зверь и каким нравом он обладает.
На предыдущих уроках я рассматривал два способа приведения. Применительно к нашему примеру:
1) Повернём эллипс на ![]() (против часовой стрелки) вокруг точки
(против часовой стрелки) вокруг точки ![]() и осуществим его параллельный перенос центром в начало координат. В результате получится нужное уравнение
и осуществим его параллельный перенос центром в начало координат. В результате получится нужное уравнение ![]() .
.
2) Перейдём к прямоугольной системе координат ![]() , которая получается путём поворота исходной системы координат
, которая получается путём поворота исходной системы координат ![]() на
на ![]() вокруг начала координат и её параллельного переноса центром в точку
вокруг начала координат и её параллельного переноса центром в точку ![]() . Таким образом, в новой системе координат
. Таким образом, в новой системе координат ![]() уравнение данного эллипса запишется в каноническом виде:
уравнение данного эллипса запишется в каноническом виде: ![]() .
.
Прошу прощения за невысокое качество и точность чертежей данной статьи:
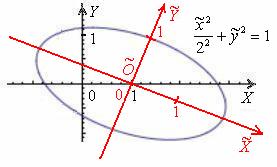
Навскидку второй способ кажется вычурным и неуклюжим, однако, если немного призадуматься, то он более корректен. И толстый намёк на это уже проскочил чуть выше: куда бы мы ни переместили данную линию, какую бы систему координат ни выбрали – эллипс останется тем же самым эллипсом с полуосями ![]() , своими фокусами и другими индивидуальными характеристиками.
, своими фокусами и другими индивидуальными характеристиками.
У многих читателей в пределах досягаемости находится учебник по высшей математике. Пусть это будет его каноническое положение в исходной системе координат. Книгу можно положить на стол, на стул, на кровать, под кровать, в мусорное ведро – да куда угодно. Но учебник останется при этом тем же самым учебником.
То есть с позиций математики, координатная сетка относительна и вторична по отношению к тому или иному объекту. Следовательно, вполне логично и правомерно тревожить именно систему координат, а не «уникальный» эллипс, учебник или что-то ещё. Конечно, с точки зрения физики положение тела имеет большое значение,… …пожалуй, сверну комментарий, а то сейчас набегут любители философии и устроят дискуссию =)
Суть преамбулы состоит в том, что на данном уроке мы будем приводить уравнение линии 2-го порядка путём перехода к новой прямоугольной системе координат, в которой уравнение исследуемой линии примет канонический вид.
Существует несколько практических методов приведения уравнения линии к каноническому виду, причём, некоторые из них являются достаточно трудными. Я постараюсь составить максимально простой конспект, доступный человеку с любым уровнем подготовки.
Все линии 2-го порядка можно разделить на две большие группы:
1) центральные линии, обладающие единственным центром (точкой) симметрии (эллипс, мнимый эллипс, гипербола, пара мнимых или действительных пересекающихся прямых);
2) нецентральные линии, у которых центры симметрии отсутствуют (парабола) либо их бесконечно много (пара действительных или мнимых параллельных прямых, пара совпавших прямых).
Итак, вы счастливый обладатель общего уравнения ![]() с ненулевым коэффициентом
с ненулевым коэффициентом ![]() . С чего начать? На первом шаге целесообразно выяснить, к какой группе относится линия. Для этого нужно мысленно либо на черновике составить и вычислить определитель
. С чего начать? На первом шаге целесообразно выяснить, к какой группе относится линия. Для этого нужно мысленно либо на черновике составить и вычислить определитель ![]() . Если
. Если ![]() , то перед нами уравнение центральной линии, если же
, то перед нами уравнение центральной линии, если же ![]() – то нецентральной.
– то нецентральной.
Для уравнения ![]() :
:
![]() , значит, оно определяет центральную линию.
, значит, оно определяет центральную линию.
Зачем это нужно? Чтобы подобрать наиболее выгодный способ решения. Конечно, если ваш преподаватель требует строго придерживаться определённого шаблона, то ничего не поделать…. Тем не менее, я постараюсь провести вас самой комфортной и короткой тропинкой через дебри.
Для приведения уравнения центральной линии, по моему мнению, лучше всего использовать метод инвариантов. Но, к сожалению, он перестаёт работать в нецентральном случае, поэтому на помощь придётся привлечь достаточно трудоёмкий универсальный способ решения либо ортогональное преобразование квадратичной формы (однако тут уже нужно ориентироваться в другой теме). Сначала разберём одно, затем другое, и даже если вам нужно разобраться только с нецентральной линией, постарайтесь не пропускать первый параграф, поскольку вся информация взаимосвязана:
Приведение уравнения центральной линии. Метод инвариантов
Во-первых, разберёмся с термином. Инвариант – это величина, которая остаётся неизменной при тех или иных преобразованиях.
Простейший пример геометрического инварианта – это длина отрезка относительно его параллельного переноса. В результате данного преобразовании меняются координаты концов отрезка, но его длина остаётся неизменной (инвариантной).
В частности, длина и ширина учебника по высшей математике (который можно положить на стол, на стул, на кровать, под кровать, в мусорное ведро) – это инварианты относительно перемещения книги в пространстве. А вот если ненавистный томик… чего студент боится больше всего? …матана порвать в клочья, то его размеры уже перестанут быть инвариантами относительно этих механических повреждений =) Но инвариантом останется сам математический анализ. Так что рви, не рви, а осваивать его придётся =)
Однако вернёмся к нашему демонстрационному уравнению ![]() . Очевидно, что можно выбрать бесконечно много других прямоугольных систем координат и получить бесконечно много разных уравнений вида
. Очевидно, что можно выбрать бесконечно много других прямоугольных систем координат и получить бесконечно много разных уравнений вида ![]() , которые задают один и тот же эллипс. И возникает вопрос: а есть ли у этого множества уравнений что-то одинаковое, характерное только для данной линии? Иными словами, есть ли инварианты?
, которые задают один и тот же эллипс. И возникает вопрос: а есть ли у этого множества уравнений что-то одинаковое, характерное только для данной линии? Иными словами, есть ли инварианты?
Да, есть! Если уравнение линии 2-го порядка задано общим видом ![]() в некоторой прямоугольной системе координат, то инвариантами относительно поворота и параллельного переноса прямоугольной системы координат являются следующие ЧИСЛА:
в некоторой прямоугольной системе координат, то инвариантами относительно поворота и параллельного переноса прямоугольной системы координат являются следующие ЧИСЛА:
![]() – сумма коэффициентов при
– сумма коэффициентов при ![]()
старый знакомец:
![]()
и ещё один определитель:
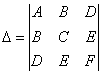
Рассмотрим общее уравнение линии 2-го порядка ![]() и поставим задачу подобрать новую прямоугольную систему координат
и поставим задачу подобрать новую прямоугольную систему координат ![]() ТАК, чтобы уравнение данной линии приняло вид
ТАК, чтобы уравнение данной линии приняло вид ![]() (который элементарно сводится к канонической форме). Заметим попутно логичную вещь – коэффициенты итогового уравнения, «отвечающие» за поворот и параллельный перенос равны нулю:
(который элементарно сводится к канонической форме). Заметим попутно логичную вещь – коэффициенты итогового уравнения, «отвечающие» за поворот и параллельный перенос равны нулю: ![]()
Поскольку инварианты (числа) ![]() НЕ ЗАВИСЯТ от коэффициентов того или иного уравнения, которым задана конкретная исследуемая линия, то справедливыми являются следующие равенства:
НЕ ЗАВИСЯТ от коэффициентов того или иного уравнения, которым задана конкретная исследуемая линия, то справедливыми являются следующие равенства:
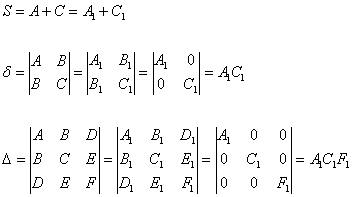
откуда следует простой и изящный алгоритм решения нашей задачи:
1) Из исходного уравнения находим числа 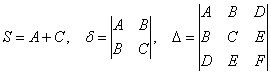 .
.
2) Решаем систему 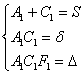 и записываем уравнение
и записываем уравнение ![]() , которое легко приводится к каноническому виду. При этом координаты
, которое легко приводится к каноническому виду. При этом координаты ![]() нового начала координат
нового начала координат ![]() отыскиваются как решение системы линейных уравнений
отыскиваются как решение системы линейных уравнений 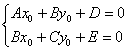 , а угол «альфа» поворота новой системы координат
, а угол «альфа» поворота новой системы координат ![]() относительно старой системы координат
относительно старой системы координат ![]() – из уравнения
– из уравнения ![]() . В случае
. В случае ![]() угол равен либо
угол равен либо ![]() , либо
, либо ![]() , и это недостаток формулы. Но это не беда. Потому что есть другая формула:
, и это недостаток формулы. Но это не беда. Потому что есть другая формула: ![]() .
.
Таким образом, решение нашей задачи укладывается в стройную и понятную схему, доступную даже школьнику. Выясним же, наконец, как из потрёпанного уравнения ![]() получается канонический эллипс
получается канонический эллипс ![]() :
:
Пример 1
Привести уравнение линии второго порядка к каноническому виду
![]()
Найти начало соответствующей системы координат и угол её поворота
Решение: перейдём к новой прямоугольной системе координат ![]() , в которой уравнение данной линии примет вид
, в которой уравнение данной линии примет вид ![]() .
.
На первом шаге из исходного уравнения находим коэффициенты ![]() .
.
В тетради это удобно сделать следующим образом:
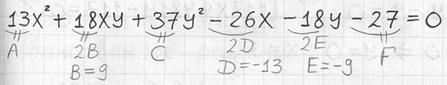
Здесь важно не потерять «минусы», а также не забыть разделить пополам нужные числа. Кроме того, некоторые слагаемые уравнения ![]() могут отсутствовать, и тогда соответствующие коэффициенты будут равны нулю – не спешим и не путаемся!
могут отсутствовать, и тогда соответствующие коэффициенты будут равны нулю – не спешим и не путаемся!
В нашем случае всё на месте и, соответственно, все коэффициенты ненулевые:
![]()
Вычислим инварианты:
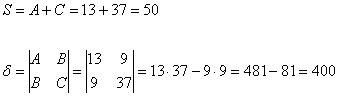
Последний определитель выгодно раскрыть с помощью элементарного преобразования, прибавив к третьей строке первую строку:
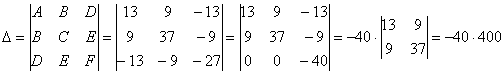
Инварианты найдёны, составим и решим систему:
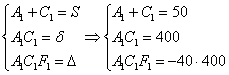
Из последних двух уравнений сразу просматривается значение коэффициента ![]() :
:
поскольку ![]() , то, подставляя это произведение в 3-е уравнение, получаем:
, то, подставляя это произведение в 3-е уравнение, получаем:
![]()
Но его обычно оставляют на закуску, тут важно разобраться с другими коэффициентами. Есть длинный путь, и есть короткий путь.
Путь длинный: из 1-го уравнения выражаем ![]() – подставляем во второе уравнение:
– подставляем во второе уравнение:
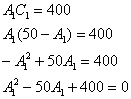
Решим квадратное уравнение:
![]()
В результате получается два комплекта симметричных корней:
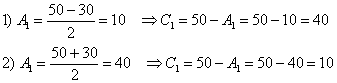
Путь короткий, к которому я рекомендую пристреляться, в том числе, и чайникам. Это подбор корней. Смотрим на первые два уравнения системы: 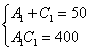 . Прикидку можно делать либо по первому уравнению, либо по второму, кому как удобнее. Лично я привык ориентироваться по сумме коэффициентов. Правдоподобных вариантов здесь не так и много:
. Прикидку можно делать либо по первому уравнению, либо по второму, кому как удобнее. Лично я привык ориентироваться по сумме коэффициентов. Правдоподобных вариантов здесь не так и много:
0 и 50
10 и 40 – удовлетворяет и первому и второму уравнению
20 и 30
30 и 20
40 и 10 – симметричная пара корней
50 и 0
Как видите, на подходящую пару чисел мы «натыкаемся» практически сразу. В силу симметричности уравнений решением будут являться и «зеркальные» значения 40 и 10.
Таким образом, в нашем распоряжении оказывается два набора корней:
![]()
Не забываем выполнить проверку, подставив значения первого (можно второго) комплекта в левую часть каждого уравнения системы:
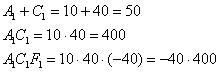
Получены соответствующие правые части исходных уравнений, что и требовалось проверить.
Теперь мысленно либо на черновике следует выяснить, какое решение приведёт нас к желаемому результату.
Подставляем ![]() в уравнение
в уравнение ![]() :
:
![]()
Техника завершающих преобразований хорошо знакома из предыдущих уроков об эллипсе, гиперболе и параболе:
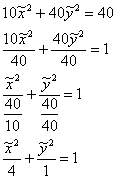
![]() – эллипс с центром в точке
– эллипс с центром в точке ![]() , большой полуосью
, большой полуосью ![]() , малой полуосью
, малой полуосью ![]() .
.
Такой фразы будет достаточно – нас никто не спрашивал про фокусы, эксцентриситет и другие характеристики линии.
Всё вышло удачно с первой попытки. Если в уравнение ![]() подставить второй набор корней
подставить второй набор корней ![]() , то получится неканоническая запись того же эллипса
, то получится неканоническая запись того же эллипса ![]() – повернутого на 90 градусов. Случай такого поворота я рассмотрел ещё в ознакомительных материалах про эллипс.
– повернутого на 90 градусов. Случай такого поворота я рассмотрел ещё в ознакомительных материалах про эллипс.
Координаты ![]() начала новой системы координат
начала новой системы координат ![]() найдём как решение системы:
найдём как решение системы:
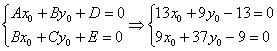
Первое уравнение умножим на 9, второе уравнение умножим на 13 и из 2-го уравнения почленно вычтем 1-е (проще способа не видно):
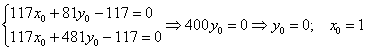
Таким образом: ![]()
Найдём угол поворота новой системы координат ![]() относительно старой:
относительно старой:
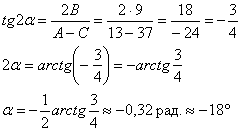
Или по второй, более лёгкой, но почему-то менее распространённой формуле:
![]()
В том случае если по условию необходимо выполнить чертёж – выполняем чертёж, приведённый в начале урока. Впрочем, мне нетрудно скопипастить:
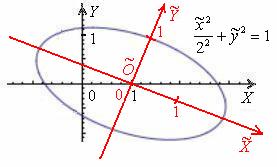
Ввиду сложности чертежа вполне допустимо его схематичное оформление, однако всё-таки постарайтесь, чтобы рисунок был похож на правду.
В лайт-варианте можно изобразить только систему координат ![]() и эллипс в горизонтальном положении, но тогда могут возникнуть вопросы у преподавателя. Да, и ещё момент – при таких раскладах координаты центра запишутся в новой системе координат:
и эллипс в горизонтальном положении, но тогда могут возникнуть вопросы у преподавателя. Да, и ещё момент – при таких раскладах координаты центра запишутся в новой системе координат: ![]() , что вызовет дополнительную путаницу.
, что вызовет дополнительную путаницу.
Ответ: ![]() – эллипс с полуосями
– эллипс с полуосями ![]() – в системе координат
– в системе координат ![]() с началом в точке
с началом в точке ![]() , повёрнутой относительно исходной системы координат
, повёрнутой относительно исходной системы координат ![]() на угол
на угол ![]() .
.
Это мы рассмотрели так называемый эллиптический случай, когда коэффициенты ![]() – отличны от нуля и одного знака (оба положительны либо оба отрицательны), т. е. когда их произведение
– отличны от нуля и одного знака (оба положительны либо оба отрицательны), т. е. когда их произведение ![]() .
.
Но при таком раскладе может получиться не только эллипс. Если все три коэффициента ![]() одного знака, то получится мнимый эллипс. Условно говоря, если бы мы в рассмотренной задаче получили уравнение
одного знака, то получится мнимый эллипс. Условно говоря, если бы мы в рассмотренной задаче получили уравнение ![]() , то пришли бы к уравнению
, то пришли бы к уравнению ![]() . Причём, весь алгоритм и порядок оформления остались бы прежними + приятный бонус – отсутствие чертежа, поскольку мнимый эллипс остаётся разве что мнить =)
. Причём, весь алгоритм и порядок оформления остались бы прежними + приятный бонус – отсутствие чертежа, поскольку мнимый эллипс остаётся разве что мнить =)
Ещё одна разновидность эллиптического случая – нулевой свободный член: ![]() , предвестником которого является нулевой третий инвариант
, предвестником которого является нулевой третий инвариант ![]() . И действительно, из 3-го уравнения системы
. И действительно, из 3-го уравнения системы ![]() следует, что если
следует, что если ![]() и
и ![]() , то нулю может быть равен только коэффициент «эф первое». Условно говоря, в нашей задаче получилось бы уравнение
, то нулю может быть равен только коэффициент «эф первое». Условно говоря, в нашей задаче получилось бы уравнение ![]() , которое легко сводится к пункту № 6 классификации линий 2-го порядка:
, которое легко сводится к пункту № 6 классификации линий 2-го порядка: ![]() – пара мнимых пересекающихся прямых с единственной действительной точкой их пересечения
– пара мнимых пересекающихся прямых с единственной действительной точкой их пересечения ![]() – с нулевыми координатами новой системы координат
– с нулевыми координатами новой системы координат ![]() .
.
Предлагаю самостоятельно ознакомиться с гиперболическим случаем:
Пример 2
Привести уравнение линии второго порядка к каноническому виду
![]()
Найти начало соответствующей системы координат, угол её поворота и выполнить чертёж.
После краткого образца решения есть важные дополнительные комментарии.
Во второй части статьи рассмотрим параболический случай ![]() , где по очевидной причине метод инвариантов становится непригодным:
, где по очевидной причине метод инвариантов становится непригодным:
Приведение нецентральной линии к каноническому виду
Сейчас мы освоим универсальный метод решения, который приближен к соответствующему теоретическому материалу стандартного курса аналитической геометрии. Таким образом, разобранные ниже задачи помогут сориентироваться не только в практике, но и лучше понять теорию.
Классический алгоритм приведения уравнения ![]() к каноническому виду вкратце состоит в следующем:
к каноническому виду вкратце состоит в следующем:
На первом шаге выясняется угол поворота исходной линии относительно своего канонического положения и осуществляется поворот исходной системы координат ![]() на данный угол. В результате в новой прямоугольной системе координат
на данный угол. В результате в новой прямоугольной системе координат ![]() уравнение исследуемой линии записывается в виде:
уравнение исследуемой линии записывается в виде:
![]()
На втором шаге выделяются полные квадраты (при необходимости), и проводится параллельный перенос системы координат ![]() началом в нужную точку
началом в нужную точку ![]() . После чего в итоговой прямоугольной системе координат
. После чего в итоговой прямоугольной системе координат ![]() получается уравнение
получается уравнение ![]() , от которого до канонической формы рукой подать.
, от которого до канонической формы рукой подать.
Должен отметить неудачные обозначения со штрихами, но так принято практически во всех учебниках, и сейчас я буду придерживаться стандарта (ну, или почти придерживаться), поскольку немалой части аудитории нужно сдавать теорию. Штрихи, как вы поняли, к производным функциям никакого отношения не имеют. В предыдущем параграфе я намеренно использовал обозначения ![]() вместо
вместо ![]() и
и ![]() чтобы не привить «чайникам» отвращение к теме.
чтобы не привить «чайникам» отвращение к теме.
Таким образом, универсальный способ приведения к линии 2-го порядка к каноническому виду предполагает два последовательных преобразования прямоугольной системы координат – поворот и параллельный перенос:
![]()
Как, наверное, все уже догадались и горестно вздохнули, удобный метод инвариантов позволял получить то же самое одним махом:
![]()
Но в параболическом случае мы вынуждены выехать с тихой просёлочной дороги метода инвариантов на оживлённую автостраду общего способа решения:
Пример 3
Привести уравнение линии второго порядка к каноническому виду
![]()
Выполнить чертёж.
Решение: в первую очередь выясним тип линии. Вычислим определитель, составленный из коэффициентов ![]() :
:
![]() , значит, у нас нецентральная линия и это может быть или парабола, или пара параллельных прямых (действительных либо мнимых), или пара совпавших прямых.
, значит, у нас нецентральная линия и это может быть или парабола, или пара параллельных прямых (действительных либо мнимых), или пара совпавших прямых.
1) Осуществим поворот исходной системы координат ![]() и переход к новой системе координат
и переход к новой системе координат ![]() ТАК, чтобы получить уравнение вида
ТАК, чтобы получить уравнение вида ![]() (без слагаемого, «отвечающего» за поворот).
(без слагаемого, «отвечающего» за поворот).
Искомый угол поворота найдём по формуле:
![]() или
или ![]()
Внимание! Данная формула справедлива только для параболического случая (![]() ).
).
В нашем примере: ![]() .
.
Вообще говоря, очевиден корень ![]() , но здесь есть одна тонкость. Наверняка многие обратили внимание на тот факт, что если линию 2-го порядка (например, гиперболу) повернуть на 180 градусов, то она совпадёт сама с собой. Исключение составляет капризная парабола, ветви которой развернутся в противоположную сторону. А парабола у нас вполне может нарисоваться, поэтому, необходимо взять на заметку ещё один угол:
, но здесь есть одна тонкость. Наверняка многие обратили внимание на тот факт, что если линию 2-го порядка (например, гиперболу) повернуть на 180 градусов, то она совпадёт сама с собой. Исключение составляет капризная парабола, ветви которой развернутся в противоположную сторону. А парабола у нас вполне может нарисоваться, поэтому, необходимо взять на заметку ещё один угол: ![]() , или, что то же самое:
, или, что то же самое: ![]() .
.
Продолжаем:
Если осуществляется поворот прямоугольной системы координат ![]() на произвольный угол «альфа» и переход к новой системе координат
на произвольный угол «альфа» и переход к новой системе координат ![]() , то формулы перехода от старых координат к новым координатам аналитически выражается следующей системой:
, то формулы перехода от старых координат к новым координатам аналитически выражается следующей системой:
![]() , где «альфа» – угол данного поворота.
, где «альфа» – угол данного поворота.
Из тригонометрических формул ![]() нетрудно выразить синус и косинус через известный нам тангенс, однако выражения получаются не однозначными:
нетрудно выразить синус и косинус через известный нам тангенс, однако выражения получаются не однозначными:
![]()
И сложившейся ситуации вполне прагматичным решением будет привлечь на помощь метод научного тыка. Не теряя времени, начинаем работать непосредственно с углом «альфа» и используем формулы ![]() . В результате дальнейших действий может получиться неканоническое уравнение (а это возможно в единственном случае – когда исследуемое уравнение задаёт параболу и та оказывается развёрнутой в другую сторону). Тогда следует рассмотреть противоположный угол поворота
. В результате дальнейших действий может получиться неканоническое уравнение (а это возможно в единственном случае – когда исследуемое уравнение задаёт параболу и та оказывается развёрнутой в другую сторону). Тогда следует рассмотреть противоположный угол поворота ![]() системы координат, при этом значение тангенса угла останется тем же самым:
системы координат, при этом значение тангенса угла останется тем же самым: ![]() , но формулы сменят знаки:
, но формулы сменят знаки:
![]() .
.
Итак, для угла ![]() выбираем первый комплект формул:
выбираем первый комплект формул:
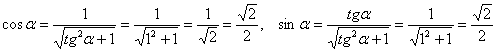
Подставим найденные (к слову, табличные) значения ![]() в аналитические выражения поворота
в аналитические выражения поворота ![]() :
:
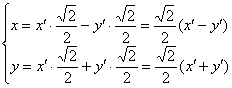
Теперь подставим ![]() и
и ![]() в исходное уравнение
в исходное уравнение ![]() :
:
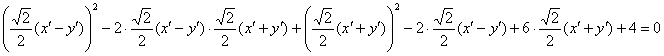
Нет причин в ужасе закрывать глаза ладонями – это ещё далеко не самое страшное, что может встретиться. Аккуратно-внимательно используем формулы сокращённого умножения, раскрываем скобки, приводим подобные слагаемые. И НЕ ТЕРЯЕМ ШТРИХИ:
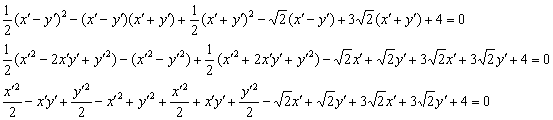
Очень многое взаимоуничтожается, и в первую очередь, конечно же, «убирается» поворот (слагаемое, содержащее произведение ![]() ):
):
![]()
По всем признакам получается как раз парабола. Сократим каждое слагаемое на 2 и перебросим некоторые из них в правую часть:
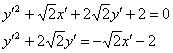
Перед слагаемым, содержащим «икс штрих», нарисовался знак минус, и это плохо. Для лучшего понимания я проиллюстрирую выполненные действия готовым чертежом:
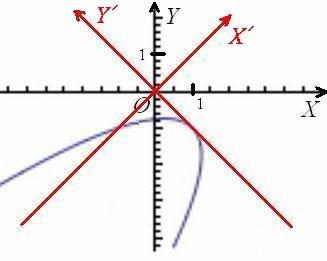
В результате поворота исходной системы координат ![]() вокруг точки
вокруг точки ![]() на 45 градусов, мы перешли от уравнения
на 45 градусов, мы перешли от уравнения ![]() к уравнению
к уравнению ![]() в новой системе координат
в новой системе координат ![]() . Но загвоздка состоит в том, что ветви параболы направлены «в противоход» оси
. Но загвоздка состоит в том, что ветви параболы направлены «в противоход» оси ![]() (наклоните головы влево на 45 градусов), о чём нам и сообщил знак «минус» при переменной
(наклоните головы влево на 45 градусов), о чём нам и сообщил знак «минус» при переменной ![]() нового уравнения.
нового уравнения.
Таким образом, выясняется, что поворот исходной системы координат ![]() следовало осуществить на угол
следовало осуществить на угол ![]() . Ну что делать, не повезло, парабола запросто могла ведь «смотреть и в нужную сторону»….
. Ну что делать, не повезло, парабола запросто могла ведь «смотреть и в нужную сторону»….
Начинаем всё сначала. Тангенс правильного «кандидата» ![]() тоже равен единице, и мы подставляем значение
тоже равен единице, и мы подставляем значение ![]() в резервный комплект формул:
в резервный комплект формул:
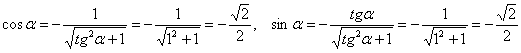
Подставим значения ![]() в уравнения поворота:
в уравнения поворота:
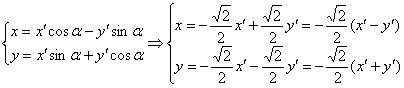
И, наконец, подставим ![]() в исходное уравнение
в исходное уравнение ![]() :
:
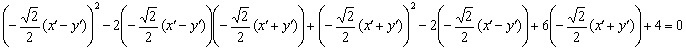
В качестве некоторой компенсации за наши мучения, для уравнения нецентральной линии существует эксклюзивная фишка, которую можно использовать как в целях самопроверки, так и по причине банальной лени. В результате рассматриваемой подстановки сумма ![]() упрощается до
упрощается до ![]() , где
, где ![]() – старый знакомый инвариант. Таким образом, громоздкая сумма первых трёх слагаемых
– старый знакомый инвариант. Таким образом, громоздкая сумма первых трёх слагаемых 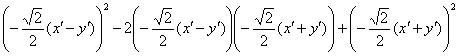 превратится в
превратится в ![]() :
:
![]()
Но при оформлении, конечно, желательно всё расписать подробно, как мы это сделали в ходе предыдущей неудачной попытки.
Доводим уравнение до кондиции:
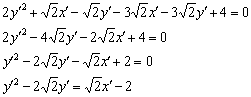
Ну вот, так бы сразу:
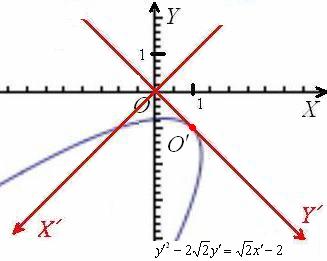
Проведём очередную разминку и заодно спасём от онемения пятую точку. Пожалуйста, встаньте лицом к монитору и наклонитесь вправо на 90 градусов. Теперь поверните голову ещё на 45 градусов в том же направлении и полюбуйтесь почти канонической параболой.
2) Осталось откалибровать уравнение ![]() до канонического вида параллельным переносом системы координат. Это значительно проще. Выделяем полный квадрат:
до канонического вида параллельным переносом системы координат. Это значительно проще. Выделяем полный квадрат:
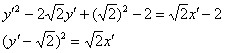
Таким образом, вершина параболы расположена в точке ![]() – ВНИМАНИЕ, это координаты точки
– ВНИМАНИЕ, это координаты точки ![]() в новой системе координат
в новой системе координат ![]() . В позе страуса с наклоном головы вправо на 135 градусов можно отчётливо разглядеть, что у вершины параболы именно такие координаты!
. В позе страуса с наклоном головы вправо на 135 градусов можно отчётливо разглядеть, что у вершины параболы именно такие координаты!
Путём параллельного переноса системы координат ![]() началом в точку
началом в точку ![]() перейдём к новой системе координат
перейдём к новой системе координат ![]() . Аналитически данное действие выражается заменами
. Аналитически данное действие выражается заменами ![]() , в результате которых получается долгожданное каноническое уравнение:
, в результате которых получается долгожданное каноническое уравнение:
![]()
Выполним окончательный чертёж. Оси ![]() совпали, но это воля случая:
совпали, но это воля случая:
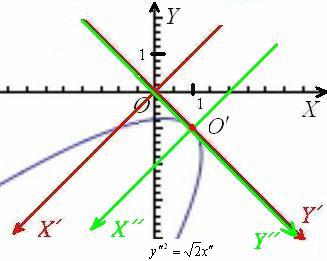
Страусы одобряют =)
Ответ: данная линия представляет собой параболу, каноническое уравнение ![]() которой получается путём поворота системы координат
которой получается путём поворота системы координат ![]() вокруг своего начала на
вокруг своего начала на ![]() и её дальнейшим параллельным переносом в точку
и её дальнейшим параллельным переносом в точку ![]() .
.
Существует ли способ проще? Существует! Изучайте квадратичные формы и урок об их ортогональном преобразовании, на котором решение этой задачи получилось заметно короче!
Также интересно отметить, что для параболы метод инвариантов, хоть и не работает, но тоже позволяет найти её каноническое уравнение. Во-первых, полезно запомнить характеристический признак: уравнение линии 2-го порядка, инварианты которого удовлетворяют условиям ![]() , задаёт параболу и только её.
, задаёт параболу и только её.
Представьте, что вы видите уравнение ![]() в первый раз. Да… с оттенком черного юмора получилась фраза =) Выпишем коэффициенты
в первый раз. Да… с оттенком черного юмора получилась фраза =) Выпишем коэффициенты ![]() и вычислим инварианты:
и вычислим инварианты:
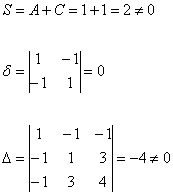
![]() , следовательно, данное уравнение определяет именно параболу, а не какую-то другую линию.
, следовательно, данное уравнение определяет именно параболу, а не какую-то другую линию.
И, во-вторых, найденные инварианты позволяют найти фокальный параметр ![]() параболы
параболы ![]() по формуле:
по формуле:
![]()
Таким образом:
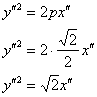
Желающие могут использовать данный путь для самопроверки или даже в качестве основного решения в критической ситуации – когда не получается найти уравнение параболы стандартным способом, но жизненно важно родить хоть что-то. Кроме того, нетрудно найти угол поворота, а там, глядишь, и прокатит.
Следующий пример для самостоятельной разработки:
Пример 4
Привести уравнение линии второго порядка к каноническому виду
![]()
Выполнить чертёж, на котором отразить все преобразования системы координат.
Краткий алгоритм решения с повторением важных моментов чуть ниже, а примерный образец оформления задачи – в конце урока.
Следует отметить, что на практике достаточно популярна урезанная версия задачи. Случай, когда нужно выполнять только параллельный перенос, досконально изучен на предыдущих уроках, но бывает и так, что требуется осуществить только поворот системы координат.
Так, например, в уравнении ![]() отсутствуют слагаемые, «отвечающие» за параллельный перенос. Угол поворота системы координат находится элементарно:
отсутствуют слагаемые, «отвечающие» за параллельный перенос. Угол поворота системы координат находится элементарно: ![]() , и, более того, с помощью «ускорителя»
, и, более того, с помощью «ускорителя» ![]() легко узнать итоговое уравнение:
легко узнать итоговое уравнение:
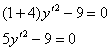
![]() – две параллельные прямые. Ещё раз подчёркиваю, что полученное уравнение имеет место в новой системе координат
– две параллельные прямые. Ещё раз подчёркиваю, что полученное уравнение имеет место в новой системе координат ![]() , повёрнутой относительно исходной системы
, повёрнутой относительно исходной системы ![]() на угол
на угол ![]() , и, соответственно, прямые
, и, соответственно, прямые ![]() будут параллельны новой оси
будут параллельны новой оси ![]() .
.
Полезно знать, что вырожденное уравнение параболического типа несложно выразить в явном виде и в исходной системе координат, поскольку проходят тривиальные алгебраические преобразования. Например:
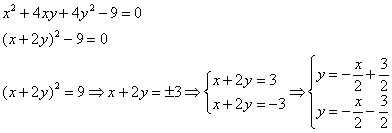
Полученный результат удобно использовать для самопроверки и выполнения чертежа.
Что касается инвариантов, то дела тут обстоят хуже. Если для параболы мы ещё смогли вытянуть некоторую информацию из инвариантов, то здесь будем созерцать малополезный набор ![]() .
.
Систематизируем порядок действий в параболическом случае::
1) Из формулы ![]() или
или ![]() находим угол поворота исходной системы координат
находим угол поворота исходной системы координат ![]() :
: ![]()
2) Для данного угла «альфа» рассчитываем ![]() . При этом проводим максимальные упрощения: выносим из-под корней всё, что можно вынести, и избавляемся от многоэтажных дробей, если таковые образовались.
. При этом проводим максимальные упрощения: выносим из-под корней всё, что можно вынести, и избавляемся от многоэтажных дробей, если таковые образовались.
3) Подставляем найденные значения ![]() в формулы поворота
в формулы поворота ![]() .
.
4) Подставляем найденные выражения поворота ![]() в исходное уравнение
в исходное уравнение ![]() , внимательно раскрываем все скобки и приводим подобные слагаемые, в результате чего в новой системе координат
, внимательно раскрываем все скобки и приводим подобные слагаемые, в результате чего в новой системе координат ![]() должно получиться уравнение вида
должно получиться уравнение вида ![]() , где
, где ![]() .
.
4*) Примерно в 15% случаев (с нецентральной линией) может получиться уравнение, которое определяет параболу, развёрнутую относительно своего канонического положения (положительного направления оси ![]() ) на 180 градусов. Тогда следует вернуться к Пункту 2 алгоритма, рассмотреть противоположный угол поворота
) на 180 градусов. Тогда следует вернуться к Пункту 2 алгоритма, рассмотреть противоположный угол поворота ![]() и использовать формулы
и использовать формулы ![]() , не забывая, что само значение тангенса осталось таким же:
, не забывая, что само значение тангенса осталось таким же: ![]() .
.
5) В полученном уравнении ![]() выделяем полный квадрат (если необходимо), в результате чего должно получиться уравнение вида
выделяем полный квадрат (если необходимо), в результате чего должно получиться уравнение вида ![]() , где
, где ![]() – некоторые константы. И, наконец, после параллельного переноса системы координат
– некоторые константы. И, наконец, после параллельного переноса системы координат ![]() началом в точку
началом в точку ![]() (замен
(замен ![]() и перехода к окончательной системе координат
и перехода к окончательной системе координат ![]() ) наша цель достигнута:
) наша цель достигнута: ![]()
6) Чертёж. Повторюсь, что во многих случаях пойдёт и схематическая версия, поскольку рисовать линии 2-го порядка под градусом – занятие нелёгкое.
И в заключение коротко об общем алгоритме решения, который годится для всех случаев, и из которого, собственно, следуют все рассмотренные выше схемы:
1) По уравнению ![]() составляем характеристическое уравнение
составляем характеристическое уравнение ![]() , где
, где ![]() ,
, ![]() – старые знакомые инварианты.
– старые знакомые инварианты.
2) Решаем квадратное уравнение ![]() и находим его корни
и находим его корни ![]() . При любых раскладах это будут действительные корни.
. При любых раскладах это будут действительные корни.
3) Данные корни определяют два угла поворота системы координат, вычисляем их тангенсы:
![]()
Теперь нам нужно выбрать нужный угол (тот, который приведёт к каноническому виду). Выбор осуществляем на черновике, методом «практического тыка». Опытные читатели могут провести анализ в уме или даже сразу «увидеть» желаемый вариант.
4) Начинаем с 1-го угла. Берём значение ![]() и рассчитываем косинус и синус этого угла:
и рассчитываем косинус и синус этого угла: ![]() . Найденные значения подставляем в формулы поворота:
. Найденные значения подставляем в формулы поворота: ![]() .
.
5) Подставляем ![]() и
и ![]() в исходное уравнение
в исходное уравнение ![]() и проводим упрощения. Если всё сделано правильно, то должно получиться уравнение вида:
и проводим упрощения. Если всё сделано правильно, то должно получиться уравнение вида:
![]() в системе
в системе ![]()
Но это может оказаться неканоническое уравнение, и тогда пункты 4, 5 следует проделать для второго угла. Кроме того, в случае с параболой есть ещё одна заморочка с углами, которую я подробно осветил в Примере 3.
6) В уравнении ![]() выделяем полные квадраты:
выделяем полные квадраты: ![]() и с помощью замен
и с помощью замен ![]() (параллельного переноса системы
(параллельного переноса системы ![]() в точку
в точку ![]() ) переходим к уравнению
) переходим к уравнению ![]() в системе
в системе ![]() . Образец сего действия неоднократно встречался ранее, в частности, в том же Примере 3.
. Образец сего действия неоднократно встречался ранее, в частности, в том же Примере 3.
7) Доводим уравнение ![]() до ума – чтобы получилось одно из девяти канонических уравнений.
до ума – чтобы получилось одно из девяти канонических уравнений.
Основная трудность общего способа состоит в его длительности и трудоёмкости, но любители сложностей могут потягать им Примеры № 1, 2. Ну а некоторые оказываются любителями поневоле :) – на первом курсе Физмата мне «повезло» с билетом по аналитической геометрии и я где-то 3 часа мучался с поворотом линии 2-го порядка, решая задачу в общем виде. Поэтому сейчас было бы просто кощунственно скрыть от вас эти знания!
Успехов!
Решения и ответы:
Пример 2. Решение: приведём данной линии к каноническому виду ![]() в новой системе координат
в новой системе координат ![]() .
.
Из уравнения ![]() находим коэффициенты:
находим коэффициенты:
![]()
Вычислим инварианты:
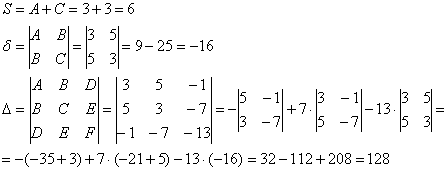
Примечание: последний определитель выгоднее раскрыть по 3-й строке либо 3-му столбцу.
Составим и решим систему:
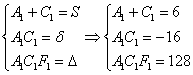
Из 1-го уравнения выражаем ![]() – подставляем во второе уравнение:
– подставляем во второе уравнение:
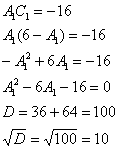
Таким образом, получаются две пары корней:
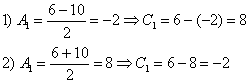
Примечание: решение несложно найти и подбором.
Подставим ![]() в третье уравнение системы:
в третье уравнение системы:
![]()
Подставляем (сначала мысленно либо на черновике!) значения ![]() в уравнение
в уравнение ![]() :
:
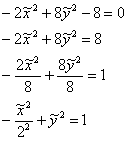
В результате получена неканоническая запись гиперболы (см. материалы параграфа о повороте гиперболы), т.е. первый набор корней нас не устраивает.
Подставляем второй комплект корней ![]() :
:
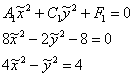
![]() – гипербола с центром в точке
– гипербола с центром в точке ![]() , действительной полуосью
, действительной полуосью ![]() , мнимой полуосью
, мнимой полуосью ![]() .
.
Примечание: опытный читатель сразу выберет 2-й комплект корней – из тех соображений, что у итогового уравнения коэффициент при ![]() должен оказаться положительным.
должен оказаться положительным.
Координаты ![]() начала новой системы координат
начала новой системы координат ![]() найдём из решения системы:
найдём из решения системы:
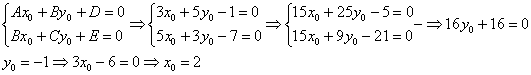
Таким образом: ![]()
Найдём угол поворота новой системы координат ![]() относительно старой.
относительно старой.
Так как ![]() , то формула
, то формула ![]() не даёт однозначного ответа об угле поворота. Поэтому используем формулу:
не даёт однозначного ответа об угле поворота. Поэтому используем формулу:
![]()
Выполним чертёж:
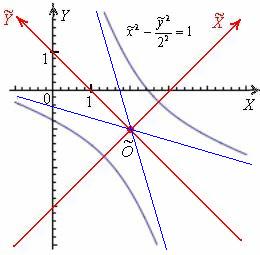
Ответ: ![]() – каноническая гипербола с полуосями
– каноническая гипербола с полуосями ![]() в системе координат
в системе координат ![]() с началом в точке
с началом в точке ![]() (координаты старой системы), повёрнутой относительно исходной системы координат на угол
(координаты старой системы), повёрнутой относительно исходной системы координат на угол ![]() .
.
Дополнительная информация: гиперболический случай выражается аналитическим условием ![]() (
(![]() и
и ![]() имеют разные знаки). Если инвариант
имеют разные знаки). Если инвариант ![]() , то коэффициент
, то коэффициент ![]() , и гипербола вырождается в две пересекающиеся прямые (пункт № 5 классификации). В нашем примере гипотетически получилось бы уравнение:
, и гипербола вырождается в две пересекающиеся прямые (пункт № 5 классификации). В нашем примере гипотетически получилось бы уравнение: ![]() – двух пересекающихся прямых
– двух пересекающихся прямых ![]() , которые, кстати, представляют собой асимптоты рассмотренной гиперболы (изображены синим цветом на чертеже).
, которые, кстати, представляют собой асимптоты рассмотренной гиперболы (изображены синим цветом на чертеже).
Пример 4. Решение: сначала выяснить тип линии. Для этого вычислим определитель, составленный из коэффициентов ![]() :
:
![]() , значит, данное уравнение задаёт нецентральную линию.
, значит, данное уравнение задаёт нецентральную линию.
Осуществим поворот прямоугольной системы координат ![]() и переход к новой системе координат
и переход к новой системе координат ![]() так, чтобы получить уравнение вида
так, чтобы получить уравнение вида ![]() , где
, где ![]() .
.
Найдём искомый угол поворота:
![]()
Если ![]() , то:
, то:
![]()
Подставим ![]() в формулы поворота:
в формулы поворота:
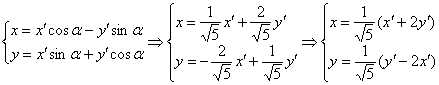
Подставим ![]() и
и ![]() в исходное уравнение
в исходное уравнение ![]() :
:
![]()
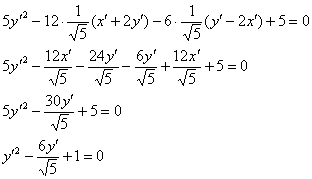
Выделим полный квадрат:
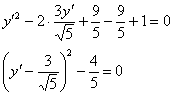
Осуществим параллельный перенос системы координат ![]() началом в точку
началом в точку ![]() . Проведём замену
. Проведём замену ![]() и запишем уравнение линии в новой системе координат
и запишем уравнение линии в новой системе координат ![]() :
:
![]() – пара прямых
– пара прямых ![]() , параллельных оси
, параллельных оси ![]() .
.
Выполним чертёж:
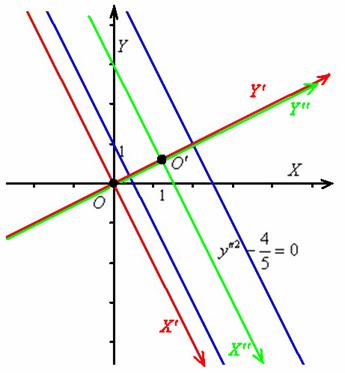
Ответ: данная линия представляет собой пару параллельных прямых, каноническое уравнение ![]() которых получается путём поворота системы координат
которых получается путём поворота системы координат ![]() вокруг своего начала на угол
вокруг своего начала на угол ![]() и её дальнейшим параллельным переносом в точку
и её дальнейшим параллельным переносом в точку ![]() .
.
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright